In a Truel with a 6-sided die, A hits with 1-2, B hits with 1-4, and C hits with 1-5. Sequence of play is A B C, skipping eliminated players. What is A's strategy, and chance to win?

Player A should aim into the air until one of B or C is eliminated.
In a duel between B and C (B first), B has a 12/17 chance of winning.
In a duel between B and C (C first), C has a 15/17 chance of winning.
In a duel between A and B (A first), A has a 3/7 chance of winning.
In a duel between A and C (A first), A has a 3/8 chance of winning.
In a duel between A and B (B first), B has a 6/7 chance of winning.
In a duel between A and C (C first), C has a 15/16 chance of winning.
If A waits, A has a 393/952 chance (42%), B has 384/952 (40%), C has 175/952 (18%). In this three player game, the weakest player has the advantage.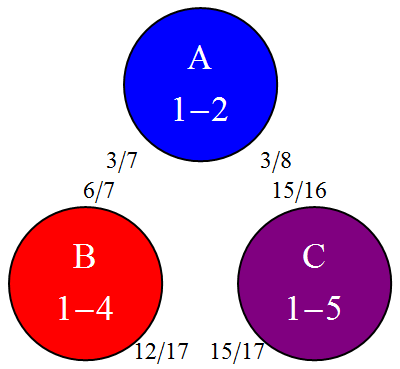