CHARLIE
          I can use a Wavelet Analysis to
          supersmooth rapid word combinations.
          
                    DON
          Start with words we understand.
          
                    CHARLIE
          Every spoken word contains phonemes -
          sounds inherent in human speech.
          Voice Recognition is based on that...
          
                    DAVID
          It keys on sounds within words
          instead of the words themselves...  

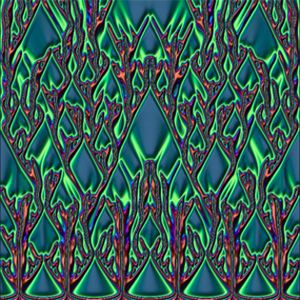
Rhymes depend on the endings of their phonetic pronunciation. The phonetic spellings of the words (buffet, cafe, okay, sleigh) all end the same way, and thus rhyme, even though their normal spellings are different. Homophones have the same phonetic spelling, as in (cinque, sink, sync) or (borough, burro, burrow). Phonetic spellings, part of Mathematica's WordData, use the International Phonetic Alphabet (IPA).

Liz at a COMPUTER TERMINAL, scrolling through a database of
suspects (generic shots). Charlie enters.
          
                    CHARLIE
          Sorry I'm late.  Amita's at a
          Combinatorics symposium in Kansas
          City and I had a lecture on
          synchronized chaos. By the way - not
          meant for one person...

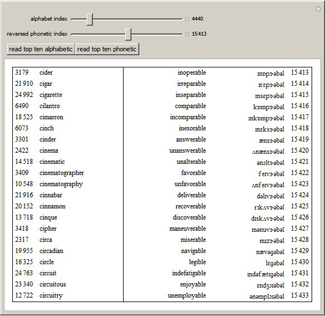
A multiset is an orderless collection of elements in which elements may be repeated, as in {a,a,b,b,c}. In this Demonstration, the elements of the multiset are arranged at the corners of a regular n-gon. Elements in the same submultiset are connected with line segments (singletons appear as dots).

                    CHARLIE
          Throwing ability aside, the
          Hyperspectral sensors collect
          information as a set of images.  These
          images are then combined to form a 3-
          D picture which reveals the objects
          true properties.

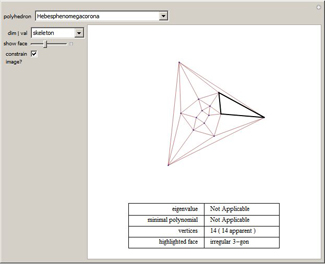
Each eigenvalue in the spectrum of a combinatorial graph's adjacency matrix gives rise to a "spectral realization" of the graph. Such a realization is both eigenic (replacing each vertex with the vector sum of its neighbors is equivalent to scaling the figure) and harmonious (each automorphism of the graph is realized by an isometry of the figure). In many cases, they are also just plain fascinating. This Demonstration reveals the spectral realizations of (the skeleton of) each named polyhedron in Mathematica's PolyhedronData[] collection.