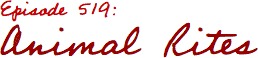LARRY
          It's called a riffle shuffle.

                    AMITA
          Larry has a history with Blackjack.

                    LIZ
          That why you won't play with us
          amateurs?

                    NIKKI
          School us, Fleinhardt.

As the women check their cards, Larry continues--

                    LARRY
          There are several categories of
          shuffle-- Stripping, Hindu, Corgi,
          Chemmy, Mongean, Faro--

In a perfect riffle shuffle, the deck is split in half and cards are alternately interleaved from each half to form a new ordering. An out-shuffle is one in which the bottom half of the deck is used to start the interleaving, so that the bottom card always remains on the bottom. With an in-shuffle, the top half is used to start the ordering. For each type of shuffle, can you find how many shuffles are necessary to return the deck to its original ordering?

As Larry speaks, Amita signals for three cards, Nikki for
two.  Liz deals them out, takes one card for herself.

                    LARRY
          Actually, Nikki makes a critical
          point.  Persi Diaconis at Stanford
          proved a minimum of five shuffles
          are required before a deck starts
          to become random in the sense of
          variation distance described in
          Markov chain mixing time, but seven
          shuffles are optimum.

                    NIKKI
          That's all I'm saying.

                    AMITA
          You think Don and Charlie got lost?
            (throwing in more chips)
          I'll bet another five.

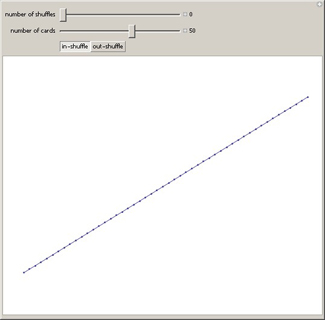
A decent first approximation of real market price activity is a log-normal random walk. But with a fixed volatility parameter, such models miss several stylized facts about real financial markets. Allowing the volatility to change through time according to a simple Markov chain provides a much closer approximation to real markets. Here the Markov chain has just two possible states: normal or elevated volatility. Either state tends to persist, with a small chance of transitioning to the opposite state at each time step.

From a doorway, Liz and David peer into a slightly darkened
auditorium filled with students listening to a LECTURER just
finishing a slide presentation on the history of the
scientific method. (slides on Galileo, his experiments, his
mathematical equations.)

                    LECTURER
          Though Galileo Galilei conducted
          research by using experiments, he
          argued his ideas in the form of
          pure mathematics...

They spot JOSH LANDON sitting across the room, crumpled in a
seat, mesmerized by the slides.  He looks more dissipated
than his photograph-- his hair is greasy and his clothes are
dirty and rumpled. (Another student sits next to him, CLOUD
JAMIESON (19) whom we will get to know soon.)

                    LECTURER (cont'd)
          ...a daring and creative evolution
          of the scientific method.  Galileo
          gave us math as proof and predictor
          of reality.

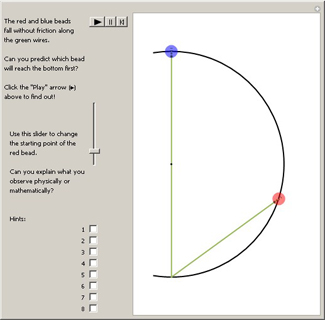
The blue bead falls straight down to the bottom of the circle along the vertical green wire. The red bead starts at a lower point and slides without fraction diagonally, finishing at the same point as the blue bead. Can you predict which bead will reach the bottom first?

Charlie and Amita pore over Josh Landon's writing.

                    CHARLIE
          His papers are filled with
          incoherent math and inductive
          argument fallacies--

                    AMITA
          In this one, he used reason to
          prove that reason is not valuable.

                    CHARLIE
          I think he has a larger intention--
            (re: a paper)
          Here's an ecological model of the
          Prisoner's Dilemma proving altruism
          in animals exceeds that of humans.

                    AMITA
          What do you think he's getting at?

Two suspects, A and B, are taken into custody by the police. The police do not have sufficient evidence for a conviction so they separate the prisoners and visit them individually to offer them the same deal. If one confesses and will testify against the other while the other still stays silent, the one who testifies will go free while the other will serve a very long time L in jail. However, if both confess, then both will spend a medium time M in jail. Finally, if both stay silent they will serve a very short period of time S in jail.