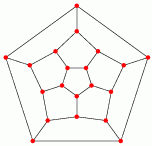
This pathfinding puzzle involves finding a Hamiltonian path. The first version of this puzzle was called The Icosian Game, developed in 1857 by Sir William Hamilton. In this puzzle, two vertices of a dodecahedron are chosen as the starting and ending points of a tour that visits every vertex exactly once. Unfortunatly, not all of the problems for the Icosian Game are solvable. The relatively rare graphs that have solutions for all starting and ending points are known as Hamilton-connected graphs. Another difficult pathfinding problem is the Traveling Salesman problem, where a shortest path through all points must be found. When all the edges of a graph must be traced, such as in "without lifting your pencil from the paper" type puzzles, it's an Eulerian path.