ENTER AUDIENCE VISION:
Anvil Head thunder clouds rise up into the sky.

                  CHARLIE (cont'd)
          In a thundercloud, frozen raindrops
          bump each other, the collisions
          creating an electric charge.

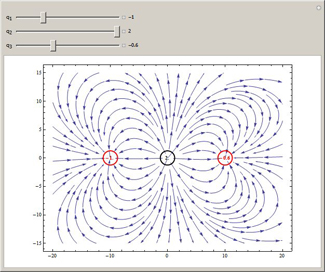
The lines of force representing this field radiate outward from a positive charge and converge inward toward a negative charge. The composite field of several charges is the vector sum of the individual fields. In this Demonstration, you can move the three charges, shown as small circles, and vary their electric charges to generate a stream plot of the electric field.

                  AMITA (cont'd)
          She says ION was going to field
          test a system that wasn't ready.
          She knew where the test would be
          and planned to watch.

                  CHARLIE
          She was struck by a plasma toroid
          device from above, indicating an
          aircraft delivery platform.

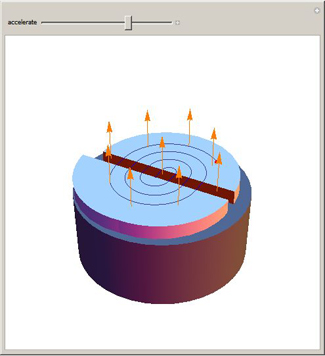
The cyclotron was invented in 1932 by Ernest O. Lawrence and M. S. Livingston at Berkeley. Particles or ions are injected into the center of two hollow D-shaped objects called "dees." A magnetic field is applied to them that is perpendicular to the plane in which they move and they accelerate across a gap between the dees by a potential difference. The orbit radius increases and eventually the particles gain energy and are ejected to hit a target. It is one of the earliest types of accelerators in use today.

                  CHARLIE
          Some sort of laser.

                  AMITA
          A laser-induced plasma channel. It
          creates a channel in the air that
          allows the system to fire a bolt of
          electricity along it.

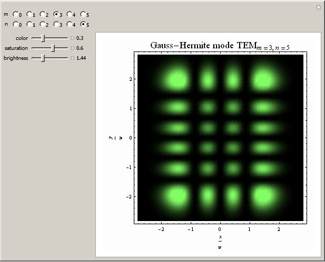
This Demonstration considers the intensity distribution of Hermite-Gaussian transverse electromagnetic (TEM) modes produced by a laser. These modes are solutions of the paraxial wave equation in Cartesian coordinates.