CHARLIE and DON lecture to a group of 20x FBI AGENTS (NIKKI
stands in back). ON SCREEN is a "Pursuit-evasion" graph, X/Y.

                 CHARLIE
          In Pursuit-evasion one group
          attempts to track down members of
          another.

                 DON
          You've just kicked in the door of a
          house looking for a third striker --

                 CHARLIE
          If you, the pursuer, occupies the
          same node as your evader, he's
          captured and removed.

ON SCREEN -- X moves into Y's space, ala PAC MAN, and takes
him out.

                 CHARLIE (cont'd)
          But, if your evader can outmaneuver
          you, then he escapes.

ON SCREEN -- Y outmaneuvers X. He exits the graph. 

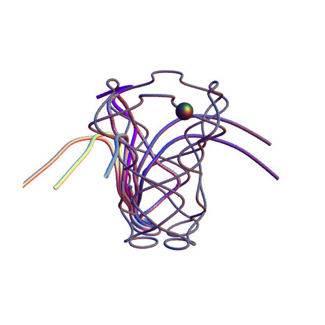
Given a moving prey (black path) with unit speed and a time-dependent position, a predator (colored path), moving with a fixed speed, runs at all times in the direction of the current position of the prey.

                 CHARLIE
          Game Theory tells us
          when someone feels they've been
          unfairly wronged, like Ian, their
          response is rarely logical.

Charlie pulls out his wallet and takes out some bills.

                 CHARLIE (cont'd)
          There's a hundred dollars here.
            (hands it to Nikki)
          A stranger told you to divide it
          between the two of us, however you
          want.

Nikki thumbs through the cash.  Gives Charlie thirty dollars.

                 CHARLIE (cont'd)
          Thirty dollars.  Really?

                 NIKKI
          No offense, but my 401K and the
          economy aren't seeing eye to eye.

                 CHARLIE
          According to the Ultimatum Game, I
          can accept or reject the offer.  If
          I reject it, neither of us gets
          anything. But I reject it anyway.
             (then)
          Any offer less then fifty-fifty and
          I'm not taking it.

He takes the money and puts it away.

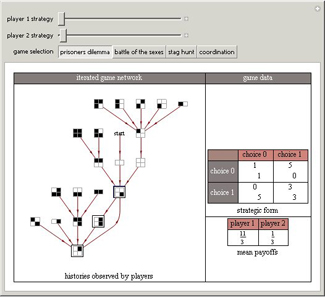
Often players in a scenario that can be modeled as a strategic form game engage in repeated interactions with each other. In such instances, their selection of a strategy on a given "iteration" may depend on their history of previous interactions. By way of example, a player might start by playing strategy 1 and continue playing it unless the history of interactions were such that the opposing player had played 0 on his/her last two turns. This Demonstration permits a selection for each player from the 2,097,152 (2^21) strategies that depend on the prior two interactions of the players. It shows the resulting "directed graph" of histories the players could observe, the steady-state cycle of histories that will be observed, the payoffs from the selected strategic form game, and the mean payoffs received by the players in the steady state.

                 DON
          He'll make unreasonable demands to
          test you out...

                 CHARLIE
          And I thought Synthetic
          Differential Geometry was
          confusing.

W. Heisenberg's real matrix group provides a noncommutative translation group of an affine three-space. The Nil-geometry, which is one of the eight Thurston three-geometries, can be derived from this group. E. Moln´r proved that the homogeneous three-spaces have a unified interpretation in a projective three-sphere.