INT. EPPES' HOUSE / LIVING ROOM - NIGHT
CHARLIE and AMITA are playing poker. He's wearing his best
pajamas. She's got a sexy Teddy under a silk robe. Charlie
lays down his cards.
CHARLIE
Beat three sixes.
AMITA puts down her cards.
AMITA
Flush. All hearts.
CHARLIE
But... you should have folded.
AMITA
I was feeling lucky.
CHARLIE
Lucky? There was a less than 18
percent probability you'd complete
the flush.

This Demonstration generates random
poker hands.
Each of the 2598960 different possible poker hands will get one of the ten possible rankings, from royal flush to
nothing.
ALAN picks up the cards, shuffles absently.
ENTER CHARLIE VISION: The cards shuffle in slow motion.
Equations are parsed into the flipping cards. The deck is
cut. THE ACE OF DIAMONDS.
EXIT VISION.
CHARLIE
(to Amita)
If we can construe each murder as a
separate Markov Chain. What if we
tried to shuffle them together?
AMITA
Analyze precipitating events and
potential motives... Find any
commonalities.

Suppose that if it is sunny today, there is a 60% chance it will be sunny tomorrow and that if it is not sunny today,
there is a 20% chance it will be sunny tomorrow. If we assume today's sunniness depends only on yesterday's sunniness
(and not on previous days), then this system is an example of a
Markov chain, an important type of stochastic process.
Charlie is in the living room with FIVE OR SIX GRADUATE
STUDENTS. There's a CHALKBOARD from the garage.
CHARLIE
I think with that we'll call it a
night. And thanks again for dealing
with the last minute change in venue.
Alan enters through the front door. Is a little surprised by
the parade of STUDENTS exiting.
CHARLIE
My Tuesday evening graduate topology
seminar.
ALAN
In our living room.
CHARLIE
We usually meet in my office, but I'm
kinda locked out at the moment.
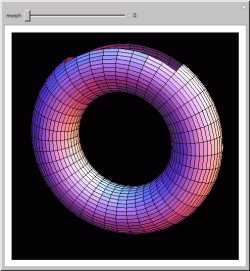
Costa's minimal surface is
described as a
torus with three points removed.
How is this done? The points are literally removed from 3D-space and flung to infinity. Here is a Demonstration of
specifically where on the torus the points are removed and how the torus turns itself inside-out when the resulting ends
of the surface are flung to infinity.
CHARLIE
There's a classic problem in
combinatorics. The Travelling
Salesman Problem...
ENTER VISION:
A VINTAGE 50s GUY WITH A VACUUM CLEANER in front of a
SUBURBAN HOME.
CHARLIE
The Salesman must visit a specific
set of cities...
A MAP OF THE US. A ROUGH OCTAGON OF CITIES ARE HIGHLIGHTED.
CHARLIE
Each leg of the trip has a different
cost...
THE CITIES ARE CONNECTED BY RAIL LINES. A PRICE APPEARS FOR
EACH CONNECTION.
CHARLIE
And he must figure out the most
routes that minimizes the total
expense.
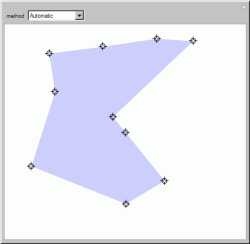
The
traveling salesman problem asks
for the shortest route by which a salesman can visit a set of locations and return home. Drag the points to change the
locations the salesman visits to see how the route changes.




