Charlie turns to the board and underlines a book title:
CHARLIE (cont'd)
For next week, chapter 15 of Theory of
Games and Economic Behavior by John von
Neumann and Oskar Morgenstern.
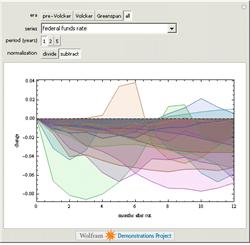
Major Federal Reserve rate cuts can have wide and varying effects on macroeconomic variables.
COLBY shows Charlie the map as they walk the floor.
CHARLIE
Fourteen locations in a five-mile
radius -- excellent. I'll get you a
probable base for the seller.
See how various location measures change as you move points around. Note that the median jumps as points change their relative coordinates. The harmonic mean is never to the right of the geometric mean, which is never to the right
of the arithmetic mean.
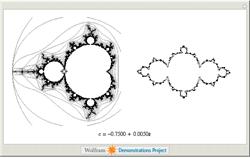
CHARLIE
Fractal Number Estimate. It's
based on Mandlebrot's use of
fractal dimension to measure the
jaggedness of a coastline. It's
been used to detect forged
handwriting, but we're applying it
because hand-drawn art can be
evaluated with the same process.
Each Julia set on the right corresponds to a quadratic polynomial of the form
f(z) = z2 + c. You can
use the locator to choose the complex
numberc from the picture of the Mandelbrot set on the left. The Julia set will be a connected set precisely when c lies in
the Mandelbrot set.
CHARLIE (V.O.) (cont'd)
The slower the pen, the longer the
contact with the paper, allowing
more ink to be absorbed. Creating a
more irregular or wrinkly edge.
The INK bleeds into the PAPER, leaves a JAGGED EDGE. GRAPHIC
FREEZES, the previous GRAPHIC of the REAL SIGNATURE SLIDES
over to be compared. A GRAPHIC OVERLAY. The SLOWER SIGNATURE
has a more 'Jagged' INK EDGE. MATH overlays and measure.
CHARLIE (V.O.) (cont'd)
Fractal Dimension allows us to
compare the wrinkliness -- and
detect which is the fake.
RETURN TO SCENE:
AMITA
These fractal comparisons are
telling us the same thing.
Choose an irrational numbers
and a horizontal unit segment with angleφ0. Define φn+1 = φn+ 2πs (mod
2π), with φ0 = 0. To the previous
segment, add a new unit segment with angle φn +
1 = θn +
φn (mod 2π). The resulting
series of line segments is the curlicue
fractal. The temperature of
these fractals measures the boundedness of these
curves. If these curves were infinitely extended, their fractal dimension would be a measure of how well they covered the plane.
DON
And you can prove this?
CHARLIE
No, but I have a theory, and it's
too elegant not to be true.
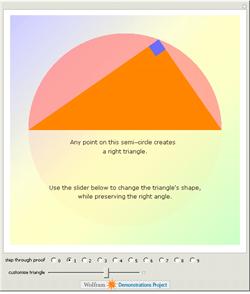
According to his autobiography, a preteen Albert Einstein devised a new proof of the Pythagorean theorem based on the
properties of similar triangles. Many
known proofs use similarity arguments, but this
one is notable for its elegance, simplicity, and the sense that it reveals the connection between length and area that
is at the heart of the theorem.
CHARLIE
Maybe, with time. But listen, I had
a hunch about the Eppes Convergence
before I had the math. Einstein
had a 'hunch' about relativity
decades before it could be proven.
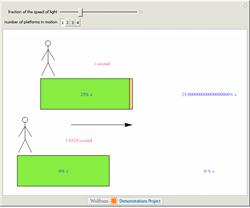
In Bertrand Russell's book The ABC of Relativity, Russell explains the following thought experiment: Suppose an
observer is on a platform at rest, a second observer is on a second platform that moves with a speed that is a fraction of the speed of light relative to the
first, a third observer moves with respect to the second with the same speed, and so on.
CHARLIE
A genuine good commingled with
false goods. In Auction Theory we
talk about equilibria or symmetry.
All bidders should have the same
exact information. But in this
case, Seth knows something the
other bidders don't know. This is
asymmetrical information. And this
can create asymmetrical bidding.
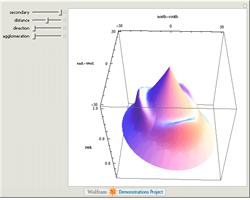
Just as the bid rent curve is not linear, neither is the earth upon which it is projected flat. The initial view shows
the cone shape of an economic topographical map arising from the bidding process as it occurs in all directions from the
center of activity. Note that the rent gradient is the rate at which rents decline as one moves away from the center in
a particular direction. The more shallow slope indicates the slower rate of rent decay and would be considered the
"path of progress." Using the secondary slider, you can see the emergence of secondary centers of activity
(there need not be three of them and they need not be equidistant from each other), creating new high-rent districts
away from the center.
