CHARLIE goes through a thick pile of files with LARRY --
CHARLIE
Wideband Mixer-Circulator Retro-Reflector.
LARRY
Obviously not...
CHARLIE
Ternary computing.
LARRY
Mmm... no.
Each rejected file going on a tall stack, next to a second,
very small one, as AMITA and ALAN enter.
A number represented in
binary is a
sum of the
powers of
2 (1, 2, 4, 8, 16, ...) multiplied by 0 or 1. For example, 60 in binary notation is
111100 = 1×32 + 1×16 + 1×8 + 1×4 + 0×2 + 0×1, using six "bits".
Balanced
ternary notation
multiplies each power of 3 (1, 3, 9, 27, ...) by -1, 0, or 1. In balanced ternary, 60
is 1
11
10 = 81-27+9-3+0, with
1 indicating -1; 60 requires five "trits".
With weights 1, 3, 9, 27, and 81, the notation can be used to balance any unit amount
from 1 to 121 by putting the weights on either side of the balance pan.
CHARLIE
With my NSA clearance suspended,
sometimes it feels like that's all I
get to do -- look.
(beat)
My next paper might very well be "Our
Friend the Triangle."
AMITA
Actually, John Conway and Steven Sigur
already wrote a great book on the
subject.
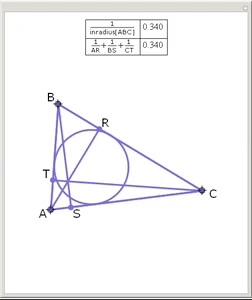
If a triangle has
inradius r
and
altitude α,
β, and
γ, then
1/
r = 1/
α + 1/
β + 1/
γ.
LARRY
I suspect I'm looking at a combinatorics
problem. Would you mind --
AMITA
Sure --
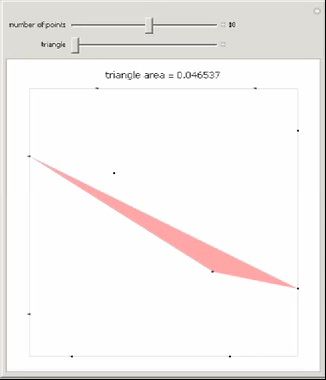
For
n points in a
unit square, find the three points that make
the triangle with minimal area. Finding the placement of
n points that produces the largest such triangle
is known as the
Heilbronn triangle problem.
The point placements shown here are the best known. Minimal triangles are colored red. All solutions
above 12 points are due to Mark Beyleveld and David Cantrell, with optimization and exact solutions found by
Mathematica.
The SAME FEEDS that were in the War Room are visible on
screens here, now -- as DON brings up the SPIDER program for
Amita and Larry --
DON
SPIDER is a --
AMITA
-- real-time ATM tracking program...
Charlie and I did work on its
Distributed Neural Network -- along
with half the Calsci math and
computer departments...
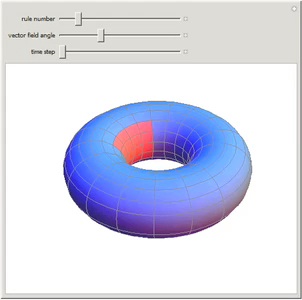
This Demonstration shows a neural network evolving under rules similar to those for a four-neighbor
outer-totalistic cellular automaton.
You can sample a variety of evolution rules exhibiting integrate-and-fire-like behavior. Red indicates
cellular activity (a neuronal spike), while blue indicates inactivity. Color intensity encodes the value
of a binary internal state variable.
COLBY
Then why risk Herman on the
kidnappings in the first place?
CHARLIE
Because he was running his own
version of a scheduling algorithm.
AMITA
(to others)
Computers use them to weigh the
duration or difficulty of different
tasks against the system's resources
and allocate them accordingly.
DON
So what does that tell us?
CHARLIE
The interesting thing about
scheduling algorithms is that no one
has come up with a perfect one.
AMITA
There are thousands -- the Smith
Rule, the O2, the Beam Search... any
programmer can design one, name it,
test it...
CHARLIE
And just like a programmer's
design... or a guitarist's signature
riff, or a painter's brush stroke...
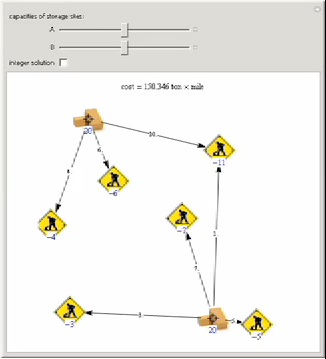
This Demonstration shows the optimal transport scheduling for two depots that are responsible for supplying
building materials to seven construction sites. Given the amount of supply available at each depot and the
demand at each site, the optimal scheduling minimizes the transport cost, assuming that the distance
between a depot and the site is the Euclidean distance.