CHARLIE
Exactly. My aggregation model will
filter through the characteristics
of the victims searching for the
strongest attributes in order to
determine their most likely choice
of seat.
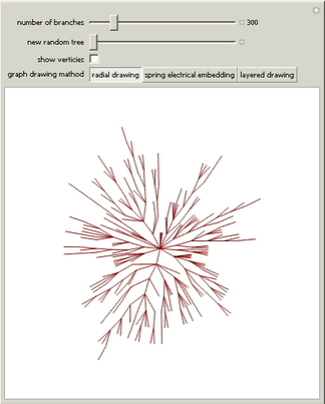
In random tree aggregation, a new
branch can be
added anywhere. Each new branch placement is selected randomly from among the
nodes already present.
LARRY
-- speaking of rearranging
molecules... did you see where
Professor Eric Kolokoff has
developed a new kind of graphene-
based digital paper...
They back against the table. Larry stares at the screen.
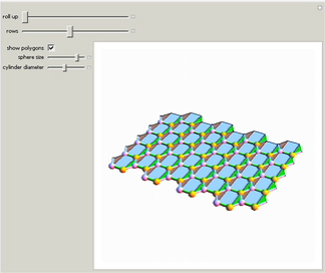
A planar
hexagonal lattice is rolled up
into a
cylinder. This can be an illustration of
how a graphene sheet forms a nanotube of "armchair" geometry.
CHARLIE
My program analyzed the DVD's...
(then)
We're cool, it's all legit. I'm
under instructions from the LAPD to
info share with the FBI.
(then)
I got results by using a Hidden
Markov Model...
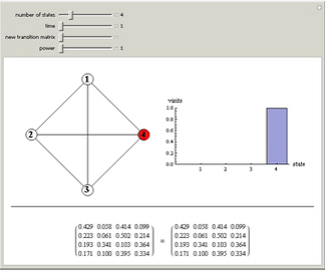
Consider a system that is always in one of
n states, numbered 1 through
n. Every time a clock ticks, the
system updates itself according to an
n×
n matrix of transition probabilities, the (
i,j)th
entry of which gives the probability that the
system moves from state
i to state
j at any clock tick. A
Markov chain is a system like this, in which
the next state depends only on the current state and not on previous states.
Powers of the transition matrix approach a
matrix with constant columns as the power increases. The number to which the entries in the
ith column converge
is the
asymptotic fraction of time the system
spends in state
i.
CHARLIE (cont'd)
-- similarly, the data you
presented appears to be an average
distribution of police work.
ON SCREEN - data appears...
CHARLIE (cont'd)
Until, like the stereogram, you
continue to stare or look at the
same data over and over again...
(data changes)
And a hidden pattern emerges.