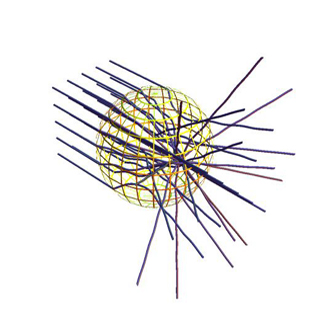
Charlie plucks a magnifying glass from a table, catches the
sunlight coming in from the windows.
CHARLIE
This magnifying glass is
transparent, right? But when light
passes through it --
The glass causes a BRIGHT SPOT SURROUNDED BY SHADOW to appear
on a piece of paper on the desk.
CHARLIE (cont'd)
-- the focal point appears to be
encircled by shadow.
The paper begins to smoke.
CHARLIE (cont'd)
The curvature of the glass bends
and focuses the light waves away
from the dark areas into that one
blinding point.
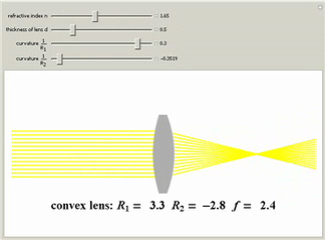
The lensmaker's equation relates the focal length of a simple lens with the spherical
curvature of its two faces, where
R1 and
R2 represent the radii of curvature of the lens surfaces closest to the light
source (on the left) and the object (on the right). The sign of
Ri is determined by the location of
the center of curvature along the optic axis, with the origin at the center of the lens. Thus for a doubly convex lens,
R1 is positive and
R2 is negative. The focal length
f is positive for a
converging lens but negative for a diverging lens, giving a virtual focus, which is indicated by a cone of gray rays.
COLBY
Underwater topography.
CHARLIE
Precisely. Now here -- yellow --
medium-size, up to two meters.
COLBY
Head-high.
CHARLIE
Red is big, up to four meters.
COLBY
Double-overhead.
CHARLIE
Purple means the waves were over
ten meters.
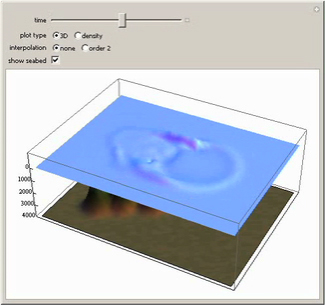
Computer modeling and simulations lead to a better understanding of natural disasters, such as the Indian Ocean Tsunami of 2004, and may prevent loss of life in the future. Using the system of
partial differential equations known as the shallow water wave equations, this Demonstration provides a reasonable approximation of the behavior of real ocean waves during a tsunami.
LARRY
So in that sense, ocean waves are
fundamentally the same as light and
sound waves -- yes?
CHARLIE
Fundamentally, yes.
LARRY
Sound waves travel at seven hundred
and sixty-one miles per hour --
CHARLIE
At sea level.
LARRY
And light waves in the vacuum of
space travel at --
CHARLIE
-- one hundred and eighty-six
thousand miles per second.
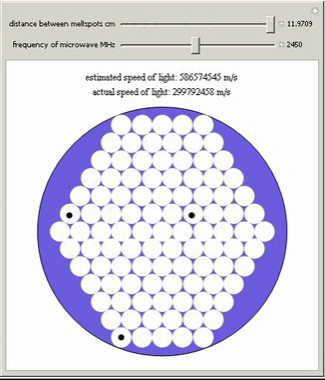
Place a plate with a single layer of marshmallows in a turntable-free microwave and zap it until some of them just begin
to melt. Measure the distance in centimeters between melt spots; it should be roughly 6 cm. Next, find a label with the
frequency of the microwave, usually 2450 MHz. With these two pieces of data, the speed of light can be calculated, via
velocity = frequency × wavelength. Chocolate chips or another substance that melts nicely may be substituted.
Without a word and in perfect synch, David and Colby play
rock-scissors-paper. David's scissors cut Colby's paper.
DAVID
I always lose when we do that. I
think you cheat.
COLBY
How do you cheat at roshambo?
DON
Charlie?
CHARLIE
I wouldn't call it cheating, but
the chaos school advocates a purely
random distribution of rock,
scissors or paper. However,
probability analysis has shown that
a mixed strategy of preconceived
gambits --
(catches himself)
You know what? I'm going to keep my
roshambo strategies to myself -- in
case I have to throw down with one
of you someday.
Rock breaks scissors, scissors cut paper, and paper wraps rock. Play against the random moves of a robot.
CHARLIE (cont'd)
I applied a deconvolution operator to
filter out spectral interference --
from other plants known to grow on the
Channel Islands -- and then I created a
neural network algorithm that could
learn to recognize known spectral
patterns based on training sets.
(beat, proud of himself)
That was the cool part.
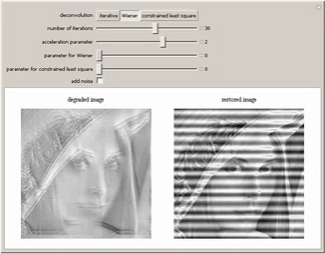
This figure shows restoration of original images from blurred images by applying various
deconvolution techniques. Photographs of people's faces on television hidden by little squares can be thought of as examples for degraded images. Vary the controls to the optimum to see an interactive restoration of the pristine image from the degraded image.