CHARLIE  (V.O.)
          Entropy.  A measure of randomness, a
          parameter of disorder... energy
          broken down in irretrievable heat.
          What might appear to be chaos... even
          decay... is really a system's way of
          smoothing out differences -- its
          search for equilibrium.  Uncorrelated 
          parts interact... find
          their connections in an evolving
          system...... so, from one perspective, 
          entropy is a clock... charting the 
          irreversible.   

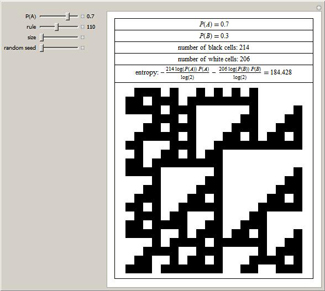
The entropy of a list Q measures its amount of disorder. The initial condition is a finite list of random bits. The entropy can be used to study the amount of information in the evolution of a cellular automaton; it is lower in ordered systems and higher in chaotic (disordered) systems.

Charlie is reading a newspaper as Amita and LARRY come in,
bringing coffee --

                    AMITA 
          Thought you snuck out early to work
          on that lecture...
          
                    CHARLIE 
          I made the mistake of buying a paper
          with my coffee.  Remember that idea I
          had for a finding in Complex
          Polynomial encryption?  Withers'
          group just patented it.
          
                    AMITA 
          It wasn't Withers... it was his
          collective.  In fact, a civil engineer
          suggested attacking it through
          Riemann's Hypothesis.

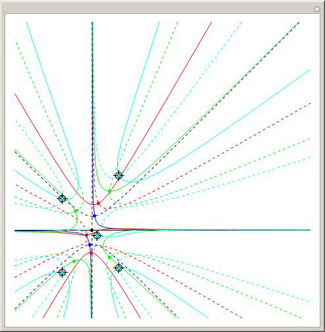
Four points in the complex plane can be the roots of a complex polynomial of degree four. Solid lines indicate where the real part is zero and dashed lines indicate where the imaginary part is zero. These lines intersect at the chosen roots. The successive derivatives of the complex polynomial behave similarly.

                    DAVID
            (thinking)
          127 rolls of floss -- which is a
          restricted item in prison for exactly
          this reason --
          
                    CHARLIE 
          We might be able to apply a Simplex
          Algorithm -- the amount of time it
          would have taken to build the ladder,
          based on difficulty of access --
          
                    LARRY
          -- they had limited time to work on
          it, when guards and other prisoners
          weren't watching them --
          
                    AMITA 
          -- they would have had to find a way
          to hide the empty containers, throw
          them out...

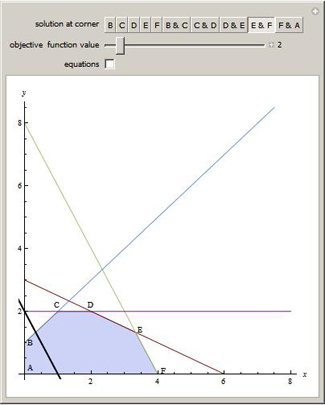
This Demonstration illustrates the graphical solution to several linear programming problems, all of which have the same set of constraints; you can vary the objective function. When two corner points are optimal, so are all the points on the line segment connecting them. The region shaded in blue is the feasible region and the colored lines correspond to the constraints. The black line represents the chosen objective function set to the slider value.

Larry and Amita give him a "no sale" look --

                    CHARLIE  (cont'd)
          Okay... I was seven years old, and I
          asked my dad to help me figure out a
          good estimate for the remainder term
          in a Taylor expansion of the
          hyperbolic cosine.  I remember our
          eyes meeting, and this... tacit
          understanding that we'd crossed the
          Rubicon.
            (beat)
          When you're seven, your father needs
          to be seven feet tall and infallible.
          So I separated math from my Dad...
          irrational as it may be, I'd prefer
          to keep it that way.

As Larry and Amita exchange a look...

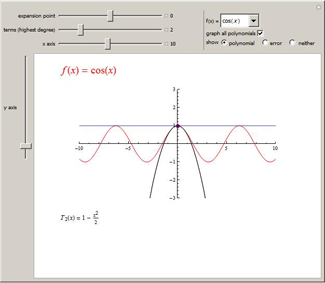
Choose the maximum degree of the Taylor polynomial to use to approximate a function. You can choose from a variety of functions and manipulate the expansion point. To see the error in the approximation, select the "error" radio button and use the slider that appears under the graph.

                    AMITA 
            (exasperated)
          Yet again, male communication tests
          the limits of Shannon's source coding
          theorem. 

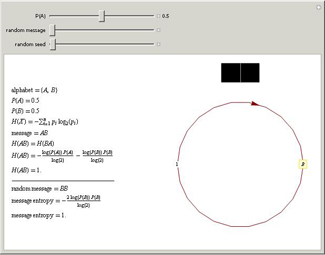
Using the second law of thermodynamics, it is possible to use random variables to calculate the information entropy (or Shannon entropy) of a message, which is a measure of the amount of information in the message. The probabilities that A and B occur in the message are P(A) and P(B).

                    CHARLIE 
          Sure... where's Maxwell's Demon when
          you need him.
          
                    ALAN
          Maxwell's Demon --
          
                    CHARLIE 
          You know -- the man who stands alone at the
          door. In two adjoining rooms, the
          temperature and pressure are the
          same... a state of perfect equilibrium.
          Every time the Demon opens the door,
          he admits only those molecules he 
          chooses... heating one room and
          cooling the other... in violation of the 
          Second Law of Thermodynamics.

Thermal energy is the energy of an object due to random motions of its atoms and molecules. The hotter the object, the greater its thermal energy. Thermal energy is an extensive variable, proportional to the size of the object. The individual molecules can have different kinetic energies, but a hot object has a higher average value. In a gas or a liquid, molecules can move freely in all directions; in a solid, molecules execute small vibrations in all directions about fixed positions.