AMITA
          Why am I the only one fascinated by
          these?  You worship Knox.  When you
          taught Ergodic Theory, you lectured
          for two weeks on his work...

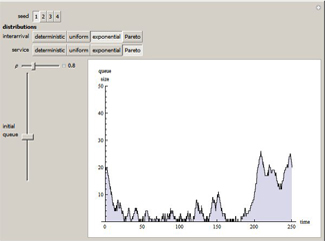
It is well known that the queue length process is ergodic only if p < 1. It is also known that when p > 1, the queue length is typically larger when there is more variability in the interarrival and/or the service time distributions.

                  ALAN
          They're making progress...

                  CHARLIE
          We found the point of convergence.
            (a nod toward Bloom)      

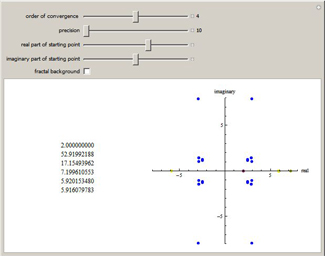
This Demonstration shows the convergence properties of a family of Newton-like methods for computing square roots of positive reals as constructed by Hernandez and Romero. In this Demonstration the roots of 35 are used. For each integer q > 2, the iterative formula (displayed in the top left-hand corner) is defined. It generates a sequence (displayed below the formula) converging to one of the roots of 35 for almost all chosen starting values in the complex plane, outside the imaginary axis. The initial point is shown in purple, the two roots (limit points) are colored yellow, and some of the intermediate points are colored in shades of yellow, with darker colors corresponding to later positions in the sequence.