UNDERWOOD
            (to Hackett)
          You look kinda familiar.

                 HACKETT
          I was at the ceremony when you were
          awarded the 15 million dollars two
          years ago. You hit Super Lotto with 2,
          7, 19, 23, 31, 41 and mega ball: 13.

                 UNDERWOOD
          How do you remember that?

                 HACKETT
          They were all prime numbers. That
          hasn't happened since the Mega
          Millions Miracle of ë98.

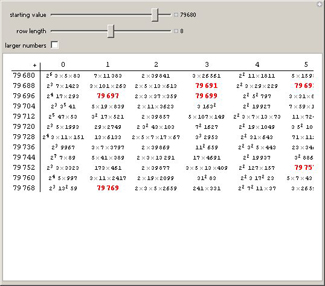
A table of prime factors, with the primes indicated in red.

                 CHARLIE
          I was right.

                 ALAN
          Still, some of the money helps fund
          schools and support teachers.

                 CHARLIE
          That's the irony. The money funds
          schools that teach, among other
          subjects, mathematics. But if more
          people understood probabilities,
          fewer would play the lottery.

                 ALAN
          People give more if they think
          they'll get something in return.

                 CHARLIE
          They're buying into a game that's
          designed to make players believe
          the odds are better than they are.
          The lottery makes you pick six
          numbers between 1 and 49. But it's
          the same as asking people to pick a
          number between 1 and 14 million.

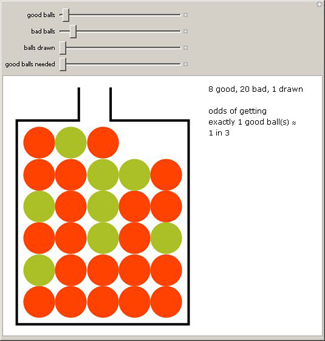
Suppose you have a lottery ticket. The ticket shows your six good balls, and there are 50 bad balls. Six balls are picked from the 56 balls in an urn. What are your chances of getting exactly 4, 5, or 6 matches? Many lotteries and gambling games are based on this concept of picking from mixed good and bad balls.

                 CHARLIE
          This is a three dimensional
          representation of the lottery's
          numerical relationship between
          ticket serial numbers and prize
          amounts. You're looking at 50 data
          points. Each one represents a
          serial number of a stolen scratchoff.
          As you can see, they appear to
          be random.

                 HACKETT
          With a limited amount of
          information, there's no way to
          determine the algorithm used to
          encode the tickets.

                 CHARLIE
          But the robbers accumulated 10,000
          serial numbers.

Hackett hits a button, the model's filled with 10,000 points.
They all line up to form a very distinct, repetitive pattern.

                 DON
          Not so random after all.

                 CHARLIE
          Once you know the pattern, you can
          crack the code.

                 HACKETT
          The robbers have enough data to
          identify the serial number of the
          jackpot ticket.

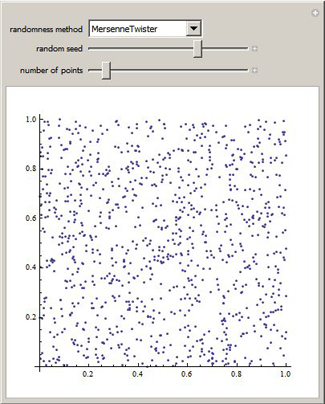
The pseudorandom methods (such as the Mersenne Twister) seem random, while the quasirandom methods (such as Sobol) seem to have a pattern, with less clustering. As an example of where quasirandom methods might be better, one method for estimating the area of a shape is to bound it, then to pick random points from that area. Using pseudorandom numbers gives the Monte Carlo method. With quasirandom numbers, the method is called quasi-Monte Carlo. Due to the relative evenness of the quasirandom methods, sometimes they give better estimates.