Set covering deployment
In "Trust Metric," Charlie attempts to aid police by finding an optimal positioning of law enforcement units patrolling downtown Los Angeles as a part of their ongoing fugitive manhunt. In Scene 15, Charlie proposes using set covering deployment to help achieve this goal:
ALAN
Charlie, didn't you do something like
this before -- chase curves --
CHARLIE
Pursuit curves... and they're not
really applicable --
(off Alan)
But you know, I've always suspected
that the Set Covering Deployment
Problem could be an invaluable aid in
positioning police units...
Set covering deployment seeks an optimal stationing of troops in a set of regions so that a relatively small number of troop units can control a large geographic region. Charles S. ReVelle and Kenneth E. Rosing first described this in 2000, in a study of Emperor Constantine the Great's mobile field army placements to secure the Roman Empire. Set covering deployment can be mathematically formulated as a (0,1)-integer programming problem. Integer programming is a special case of linear programming, which refers to optimizing an outcome based on some set of constraints using a linear mathematical model, and (0,1)-integer programming means that all variables are required to be integers equal to either 0 or 1--in other words, the variables are binary.
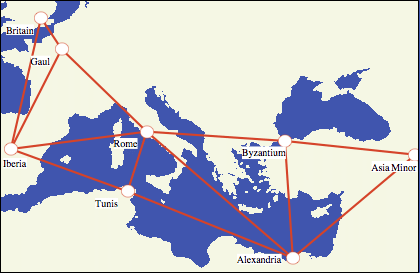
To formulate the Roman domination problem, consider the 8 provinces of the Constantinian Roman Empire illustrated above. Each region is represented as a white disk, and the red lines indicate region connections. Call a region secured if one or more field armies are stationed in that region, and call a region securable if a field army can be deployed to that area from an adjacent area. In addition, assume that a field army can only be deployed to an adjacent region if at least one army remains in the original region to provide logistical support. Also assume that each region contains at most two armies, as the number of available armies are limited and cannot be concentrated in any one region.
This problem can then be mathematically formulated by representing the Empire as a graph. Note that here, the word "graph" is
a mathematician's usage of the term: not a plot of a function, but rather a collection of points (the vertex set V) and lines (the edge set E) connecting some subset of the
points. We can then associate two binary variables 
and 
with each vertex 
(i.e., each province) in the vertex set 
of the Roman Empire graph
which specify whether a first and second field army (respectively) is located at a given vertex .
In the terminology of graph theory, the Roman Empire graph is a simple connected graph on eight vertices and with 13 edges. Here are several types of undirected graphs, including some particularly attractive named graphs encountered in mathematical graph theory. (To learn more about these graphs, click on their images.)
In set covering deployment, the problem to be solved is to maximize the quantity 
subject to the constraints
which guarantees that the first legion is stationed at a given vertex before a second can be,
which guarantees that if does not
contain a field army, it has a neighbor with two field armies, and
which enforces the integer constraint (i.e., when combined with the first constraint, only zero, one, or two field armies may be placed in any given region). This integer programming problem can then be translated into matrix terms and solved using standard techniques to find the minimum number of field armies needed to secure the Constantinian Roman Empire.
The lighthouse analogy
In reality, Charlie's optimization problem is somewhat different: to maximize the area that can be reconnoitered by a fixed-size police force in downtown Los Angeles. It's different because police may assume any positions instead of being restricted to a set of discrete locations, and because it involves no secondary considerations such as "empty" regions requiring two neighboring police units to be present. Charlie describes it using the analogy of lighthouses:
CHARLIE (cont'd)
But lighthouses are a limited
resource; they cost time, money,
materials. Using Set Covering
Deployment --
-- boom up into an AERIAL OF THE COASTLINE (not a straight
line, but jagged) -- the sweeping lights becoming CIRCLES OF
LIGHT, intersecting --
-- we determine the best placement of
our limited number of lighthouses to
illuminate the ocean.
-- the circles connecting by lines, becoming a geometrical
organization that blankets the coast.
Covering problems
Charlie's lighthouse model describes what is mathematically known as a covering problem: given a set of geometric shapes, find an arrangement that maximizes the fraction of a specified area that they can cover. In the case of lighthouses, the region of the coast covered is the fraction from which at least one lighthouse can be seen. In the case of police officers in downtown Los Angeles, to first approximation (ignoring local topography such as streets, building, etc.) we can assume that each officer "covers" a circular region (i.e., a disk) whose size is proportional to the distance that officer can see (or run). Taking the search region as a square set of city blocks (shown in gray below), the following visualization shows a configuration of randomly distributed police officers with random coverage radii, giving an arrangement that covers only 50% of the search region.
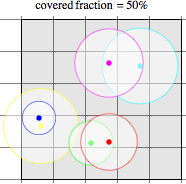
Obviously, the larger the size of the police force and the larger the coverage radii of individual police units, the
higher the fraction of area that can be covered. However, optimal placement gives the best coverage possible
for a fixed set of police units. In the case above, it turns out to be possible to arrange the six disks so that they
have no overlap, so the maximum coverage is given by 
, i.e., the sum of the
disk areas, each of which is given by
times the
radius squared, where radii are measured in units of the edge length of the square.
In general, achieving optimal coverage requires minimizing disk overlap, as well as minimizing the amount by which disks extend outside the area of surveillance. As you can see below, an optimal solution is not necessarily unique; in this case, there are several separate disk arrangements that all share an optimal 69% coverage. You can interactively explore optimal coverages for different numbers of police units using the applet at the top of this page.
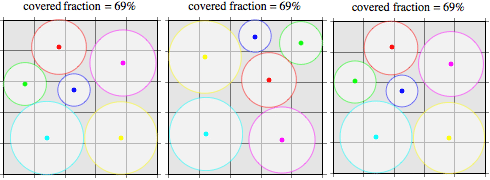
Global optimization
Covering problems are a form of global optimization problem. In general, such problems are difficult to solve even approximately, let alone exactly. In the more complicated case of placing even as many as ten police, one can imagine moving them around "by hand." But in general, as the number of objects becomes large, problems of this type become unmanageable using not only "hand" methods, but also using any sort of combinatorial methods. Effective practical methods are thus needed.
As seen above in the case of Roman domineering, addressing a problem mathematically generally requires two steps: (1) formulating the problem mathematically and (2) using appropriate methods to find a solution. Depending on the nature of the problem, one of these steps may be harder than the other. In the idealized police deployment problem, step 1 is "easy," as the problem can be rather succinctly formulated as maximizing the function
![I(x_1, ..., x_n) = int_{[0,1]^2} [[vee_{i=1}^n (|x-x_i| < r_i)]] dx dy](images/index_20.gif "I(x_1, ..., x_n) = int_{[0,1]^2} [[vee_{i=1}^n (|x-x_i| < r_i)]] dx dy"){kind=small}
--that is, finding the set of points 
constrained to the unit square (
) that give
, where ![[[S]]=cases{0 if S is false; 1 if S is true](images/index_24.gif "[[X]]=cases{0 if S is false; 1 if S is true"){kind=small}
is the Iverson bracket, 
denotes a vector
norm, and ∨ is the logical OR operator. Here,
we have made the assumptions that a given police officer's covering radius 
is fixed regardless of the officer's position, and
that we know or can estimate a value of this radius for each police officer. Finally, the symbol ![\int_{[0,1]^2} ... dx dy](images/index_26.gif "int_{[0,1]^2} ... dx dy"){kind=small}
denotes a double integral over the unit square that gives the total amount of area covered by police. So the
mathematical formulation above simply says, "For a given set of police positions and coverage radii, find all
regions in the unit square covered by at least one police officer, sum their areas (making sure to count regions of
overlap only once), and maximize this area for fixed radii over all possible police positions."
Once the problem has been mathematically formulated, it can be solved using one of a number of optimization algorithms, such as the following (all of which, incidentally, are built into the Mathematica command NMaximize):
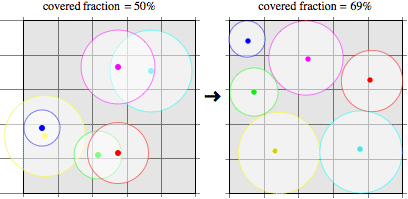
In this case, applying differential evolution to a set of initial police positions improves the coverage from 50% to an optimal 69%.
Mathematical covering problems
 |
|
 |
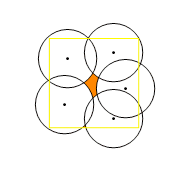Specific covering problems are also a source of mathematical investigation. One such problem is the so-called disk covering problem: given n identical disks, find the smallest possible radius r(n) such that there exists an arrangement of the disks that (just) completely covers the unit disk. Note that this is actually a different problem from the lighthouse or police coverage problems mentioned in the script, in which we are asked to assume that a shape (i.e., the California coast, or downtown Los Angeles) is of fixed size and is independent of the number of disks, and the problem posed is to find an arrangement of disks that provides optimal (or, practically speaking, as good as practically possible) coverage. |
 |
|
In the case of trying to apply a numeric algorithm to find r(n), it is necessary to reliably optimize a packing for a given radius, then vary the radius until 100% coverage can no longer be achieved. As a result, this is actually a much harder problem than covering a fixed shape optimally, especially as n increases. In fact, while the cases of n = 1 to 4 are trivial, r(5) is already quite difficult, and while its exact solution has been proved mathematically (illustrated below; it turns out to be very slightly smaller than the radius covered by five symmetrically arranged disks--the so-called five disks problem), minimal radii are not even known for almost all larger n.
INT. FBI - WAR ROOM - MOMENTS LATER
More-complicated heuristics
Of course, the idealized mathematical problem we set up and solved for police coverage ignored real-world considerations such as the presence of buildings, busy streets, and other obstacles; the difficulty in estimating the coverage radii for a set of police officers; and so forth. In a refinement of their initial lighthouse model, Charlie and Amita incorporate more-complicated heuristics into an algorithm with help from Larry:
LINES show up from various points, with different widths --
paths with various branches -- swaths of colored light, also
with mathematical notations -- creating loose geometric
patterns --
LARRY
As we receive more data, we can
better predict and weight possible
travel paths... of course, it must
look fairly abstract --
This enhanced algorithm is what ultimately allows Don to identify the subway tunnels as a likely hiding place in Scene 30:
DON (cont'd)
Why do you have such low values on
the subway stations?
CHARLIE
Coverage -- there are police on the
station stairs and platforms, others
riding the trains back and forth...
DON
... but not the tunnels...
(tracing the route)
And with some Hollywood magic, that's exactly where he locates Colby and Carter in Scene 31!
INT. FBI - WAR ROOM - DAY
Illumination problem
In Scene 47, Charlie is attempting to determine where fugitive Carter has fled. He has an inspiration that Carter may not have run to the Chinese Embassy, but instead to a ship making its way out of U.S. territorial waters:
CHARLIE
Ernest Straus posited a roomful of
mirrors...
... Straus wondered if there was a
room so complex that a match lit in
the right place couldn't reach every
corner?
It was forty years before George
Tokarsky devised an answer -- a 26
sided room...
(beat)
... and, in the spirit of that
problem, and solution, I looked for
Carter's dark corner -- the nearest,
safest Chinese soil.
The general problem that Charlie refers to is known as the illumination problem, proposed in the early 1950s by Ernst Straus.
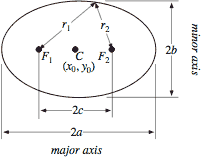
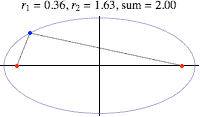
In 1958, a young Roger Penrose used the properties of the ellipse to describe a room with curved walls that would always have dark (unilluminated) regions, regardless of the position of the candle. Before we discuss this room in more detail, recall that an ellipse is an oval-shaped figure that can be defined as the set all points in a plane whose distances from two fixed points (known as the foci) sum to a positive constant, as illustrated below.
|
|
 |
 |
Ellipses aligned along the Cartesian coordinate axes are described by the equation
where a and b are, respectively, half of the major and minor axes of the ellipse, known as the semimajor axis and semiminor axis. Ellipses arise in many physical contexts, including as the shape of planetary orbits in Newton's theory of gravitation. They also have a large number of intriguing mathematical properties, including the fact that any ray of light passing through a focus and reflecting off the walls of an ellipse will pass through the other focus after a single bounce.
Penrose's room is illustrated below, and consists of two half-ellipses at the top and bottom and two mushroom-shaped protuberances (which are in turn built up from straight line segments and smaller half-ellipses) on the left and right sides. The ellipses and mushrooms are strategically placed as shown, with the red points being the foci of the half-ellipses. There are essentially three possible configurations of illumination. In this figure, lit regions are indicated in white, unilluminated regions are indicated in gray, and the position of the light source is indicated by the black cross-hairs. As can be seen, the entire room (the space within the blue border) can never be fully illuminated.
After Straus's question had thus been answered in the negative for arbitrarily shaped rooms, the more restrictive problem of rooms required to have walls composed of straight line segments remained open. In particular, in 1969, Victor Klee publicized these questions:
Both questions remained open until 1995, when George W. Tokarsky showed that unilluminable straight-walled rooms exist in two and three dimensions. Interestingly, question (2) remains open. The smallest known counterexample to (1) found by Tokarsky in two dimensions has 26 sides, and is illustrated below. It should be noted that the Tokarsky room is a borderline case, because in actuality a finite number of dark points remain unilluminated when a point light source is placed at a given position. So for an extended light source, this room actually is illuminable. The path of light beams for a number of different candle positions and beam orientations in Tokarsky's room are animated below. An even small counterexample--a room with 24 sides--was subsequently found by Castro in 1997; see MathWorld for an illustration.
Mathematical billiards
Illumination problems are intimately related to billiards. The reflection of light from the surface of a mirror is exactly analogous to the reflection of a billiard ball from a cushion of a billiard table because the so-called law of reflection--which states that the angle of incidence equals the angle of reflection--applies equally in both cases. There is some very interesting math involved in billiards. In fact, analysis of billiard paths can involve sophisticated use of powerful mathematical tools such as ergodic theory and dynamical systems.
An interesting result in billiard-table mathematics is that on an elliptical billiard table, the envelope of a trajectory is a smaller ellipse (top left figure), a hyperbola (top middle figure), a line through the foci of the ellipse (top right figure), or a closed polygon (bottom figures). The closed-polygon case is related to a remarkable geometric result known as Poncelet's porism. An interactive exploration of the elliptical billiard table is available from The Wolfram Demonstrations Project.
EXT. CALSCI FACULTY CLUB - DAY
Summing up with an equation
AMITA
Sounds like an addendum to "The
Mathematics of Friendship."
LARRY
I'm not familiar with that paper --
ALAN
Early Charles Eppes -- friendship as
an equation...
DON
... a self-improvement manual for
eggheads.
While Charlie, Alan, Don, Larry, and Amita could undoubtedly engage in an enlightening conversation over beer and pizza about the mathematics of billiards, they instead close this episode by discussing Charlie's work on the mathematics of friendship. We will not attempt to derive Charlie's "friendship equation" here due to limitations of space and time, but perhaps Charlie will have more to say on this topic in upcoming episodes!
References
Castro, D. "Corrections." Quantum 7, 42, Jan. 1997.
Croft, H. T.; Falconer, K. J.; and Guy, R. K. "Illumination Problems." §A5 in Unsolved Problems in Geometry. New York: Springer-Verlag, pp. 18-19, 1991.
Gardner, M. The Second Scientific American Book of Puzzles & Diversions: A New Selection. New York: Simon and Schuster, pp. 142-144, 1961.
Ingber, L. "Simulated Annealing: Practice Versus Theory." Math. Comput. Modelling 18, 29-57, 1993.
Kirkpatrick, S.; Gelatt, C. D.; and Vecchi, M. P. "Optimization by Simulated Annealing." Science 220, 671-680, 1983.
Klee, V. "Is Every Polygonal Region Illuminable from Some Point?" Math. Mag. 52, 180, 1969.
Nelder, J. A. and Mead, R. "A Simplex Method for Function Minimization." Comput. J. 7, 308-313, 1965.
Neville, E. H. "On the Solution of Numerical Functional Equations, Illustrated by an Account of a Popular Puzzle and of its Solution." Proc. London Math. Soc. 14, 308-326, 1915.
ReVelle, C. S. and Rosing, K. E. "Defendens Imperium Romanum: A Classical Problem in Military Strategy." Amer. Math. Monthly 107, 585-594, 2000.
Rubalcaba, R. R. "Fractional Domination, Fractional Packings, and Fractional Isomorphisms of Graphs." Ph.D. dissertation. Auburn, Alabama: Auburn University. May 13, 2005. http://webpages.uah.edu/~rubalcr/RUBALCABA.pdf
Sprott, J. C. "Dynamical Models of Love." Nonlin. Dyn., Psych., Life Sci. 8, 303-313, 2004. http://sprott.physics.wisc.edu/pubs/paper277.pdf
Sprott, J. C. "Dynamical Models of Happiness." Nonlin. Dyn., Psych., Life Sci. 9, 23-36, 2005. http://sprott.physics.wisc.edu/pubs/paper281.pdf
Tokarsky, G. W. "Polygonal Rooms Not Illuminable from Every Point." Amer. Math. Monthly 102, 867-879, 1995.
