CHARLIE
I had this idea that I could navigate
the 11th Grade with the minmax
theorem and n-person games.

          AMITA
Did it work?

          CHARLIE
My insights into the network
externalities of school elections
were bulletproof. Payoff Strategies
for doing other people's homework
were not quite as well reasoned.

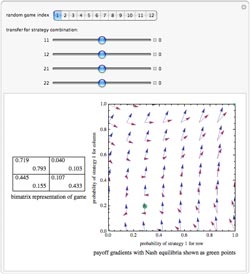
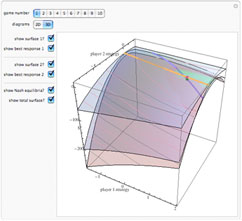
In a strategic form game, each player's payoffs are a function of the combination of their probability distributions over their sets of strategies.

          ALAN
Charlie, didn't you do something like
this before -- chase curves?

          CHARLIE
Pursuit curves... and they're not
really applicable --

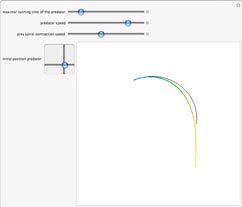
Given a moving prey (black path) with unit speed and a time-dependent position {x(t), y(t)}, a predator (colored path), moving with speed v, runs at all times in the direction of the current position of the prey.

          CHARLIE
... a coastline at night. To keep us
from crashing on the rocks, we build
lighthouses.

But lighthouses are a limited
resource; they cost time, money,
materials. Using Set Covering
Deployment --

-- we determine the best placement of
our limited number of lighthouses to
illuminate the ocean.

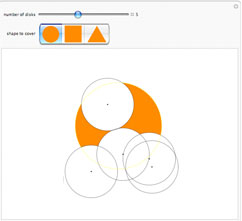
Completely cover the orange shape with the white disks. The number of disks determines the size of each shape.

          ALAN
Makes sense -- there must be some
mathematical term for removing the...
clutter --

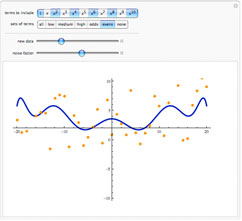
Polynomials can be used to fit noisy data. This Demonstration allows you to explore the relationship between the terms in a fit and the shape of the fit. You can experiment with different sets of powers.

         CHARLIE
Ernest Straus posited a roomful of
mirrors...

... Straus wondered if there was a
room so complex that a match lit in
the right place couldn't reach every
corner?

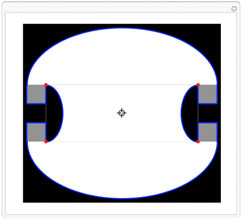
In the early 1950s, Ernst Straus asked if a single candle could illuminate an entire room made with mirrored walls, no matter what the shape of the room.

         CHARLIE
It was forty years before George
Tokarsky devised an answer -- a 26
sided room...
    (beat)
... and, in the spirit of that
problem, and solution, I looked for
Carter's dark corner -- the nearest,
safest Chinese soil.

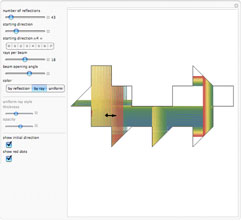
If a candle is inside a room with mirrored walls, can any portion of the room be dark? In 1958, a young Roger Penrose found an unilluminable room with elliptical sides.