

Snell's law
In the episode "Hollywood Homicide," Charlie must help identify a murder victim found submerged in a bathtub. Fortunately, a home video provides a distorted image of the victim's face, so Charlie can apply a number of different techniques to attempt to correct for the distortions in the image.
Charlie nods toward the screen.
CHARLIE (cont'd)
It's the same with this image.
It's being scattered by the forces
of refraction... But using Snell's
Law, a dash of Goos-Haenchen shifts
and a motion-tracking algorithm...
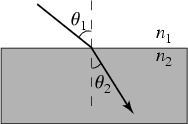
Snell's law gives the relationship between the angles of incidence ![]() and refraction
and refraction ![]() for a wave impinging on an interface between two
different substances. Note that by convention the angles here are measured not from the surface of the interface, but
rather from the normal to it (i.e., from the vector perpendicular to the surface, indicated by the above dashed
line), and the relevant function is the well-known sine function, beloved by trigonometry students. Because light travels at different speeds through different substances, the
laws of physics require that a wavefront of light gets bent as it slows down or speeds up upon entering a
different medium. This bending is known as refraction, a phenomenon familiar to anyone who has noted the apparent
offset of a penny at the bottom of a swimming pool (or even an olive in a martini glass!) when viewed from above.
for a wave impinging on an interface between two
different substances. Note that by convention the angles here are measured not from the surface of the interface, but
rather from the normal to it (i.e., from the vector perpendicular to the surface, indicated by the above dashed
line), and the relevant function is the well-known sine function, beloved by trigonometry students. Because light travels at different speeds through different substances, the
laws of physics require that a wavefront of light gets bent as it slows down or speeds up upon entering a
different medium. This bending is known as refraction, a phenomenon familiar to anyone who has noted the apparent
offset of a penny at the bottom of a swimming pool (or even an olive in a martini glass!) when viewed from above.
Every physical substance can be characterized by its index of refraction n, which is simply a measure of how fast light travels in that substance, expressed as n = c / v, where c is the speed of light in a vacuum (which, according to Einstein's special theory of relativity, is the fastest speed at which any physical object can travel or at which energy/information transmission can occur) and v is the speed of light in the given substance (which, in general, is also a function of wavelength). A large index of refraction means that light travels more slowly. For instance, while air's index of refraction (nair) is very close to 1, nwater = 1.33. This is because light travels almost as quickly in air (which is very thin) as it does in a vacuum, but travels more slowly in the thicker medium of water.
Snell's law follows from continuity conditions on electromagentic fields across the interface boundary. It may also be derived from an even more general concept known as Fermat's principle. In its modern formulation, Fermat's principle states that a light ray going between two pointss must traverse an optical path length that is stationary with respect to variations of the path, where stationary is a mathematical term meaning the paths may be maxima, minima, or saddle points.
The form of Snell's law suggests the possibility of a phenomenon in which incident light is not refracted at
all, but rather is completely reflected. This phenomenon does occur and is known as total
reflection. Total internal reflection is the reflection of electromagnetic radiation encountering an
interface where the new substance has a larger index of refraction than the radiation's current medium. This form of
reflection occurs for angles satisfying ![]() --precisely the
situation in which the relationship required by Snell's law can no longer be mathematically satisfied. For typical
wavelengths and interfaces, air has a lower index of refraction and other media have larger indices of refraction, so total internal
reflection is the form of total reflection normally encountered. For X-rays, on the other hand, a solid medium is
optically less dense than a vacuum, producing instead a total external reflection.
--precisely the
situation in which the relationship required by Snell's law can no longer be mathematically satisfied. For typical
wavelengths and interfaces, air has a lower index of refraction and other media have larger indices of refraction, so total internal
reflection is the form of total reflection normally encountered. For X-rays, on the other hand, a solid medium is
optically less dense than a vacuum, producing instead a total external reflection.
Goos-Hänchen effect
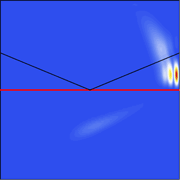 |
In his comments to Larry, Charlie also mentions Goos-Hänchen shifts. In 1947, F. Goos and H. Hänchen experimentally showed the surprising fact that a light beam totally reflected from an interface of two substances is laterally displaced from the position predicted by pure geometric reflection. The next year, this effect was explained theoretically by K. Artmann. The resulting phenomenon, now known as the Goos-Hänchen effect, is illustrated in the animation at left, in which the reflection of an elongated moving Gaussian packet has been calculated in Mathematica. The shift of the packet's center relative to the position expected from pure geometric reflection is clearly visible. |
In 1955, F. Fedorov argued that a transverse displacement of a totally reflected beam should also occur. This displacement was calculated theoretically by C. Imbert in 1972 using an energy flux argument. In their honor, this phenomenon is usually called the Imbert-Fedorov effect. Both the Goos-Hänchen and Imbert-Fedorov effects have received quite a bit of theoretical and experimental investigation in recent years. However, as these effects are very small (in fact, the offsets they produce are typically on the same scale as the wavelength of light), they are extremely difficult to detect experimentally, especially in the optical domain (where wavelengths are roughly in the range of 400-750 nanometers, which is about the diameter of an E. coli bacterium). We therefore presume that while Snell's law could certainly be relevant in his analysis, by referring to Goos-Hänchen, Charlie is indulging in a bit of physical hyperbole for Larry's benefit rather than suggesting that this effect has any practical implications for naked-eye observations of bathtubs.
Archimedes' principle
CHARLIE
Perfect. I may be able to tell you
the killer's size.
ALAN
Charlie, how are you gonna do that?
CHARLIE
Displacement. Remember I was
cleaning the tank...
ALAN
Well, obviously, Charlie, the water
level drops.
CHARLIE
Yes. By an amount exactly equal to
the volume of this rock.
Archimedes' principle of buoyancy states that the buoyant force exerted on a floating body is equal to the weight of the volume of liquid displaced by that body, meaning that a floating body displaces exactly its weight in a liquid. This principle is named after the greatest mathematician of ancient times, Archimedes of Syracuse (ca. 287-ca. 212 BC). Legend has it that Archimedes discovered his principle of buoyancy while taking a bath, upon which he is supposed to have run naked and dripping through the streets of Syracuse shouting "Eureka!" (a fact referred to previously by Larry in Episode 231, "All's Fair"). The weight of water is about 62.4 pounds per cubic foot, so one could in principle tell the weight of a person floating in a bathtub based on how much the water level rises.
However, Archimedes' principle applies only to a body having density less than that of the fluid in which it is immersed, i.e., a floating body. If the body is instead denser than the surrounding liquid, it will sink and, instead of displacing its own weight of liquid, it will simply displace its own volume of liquid. Furthermore, if the body rests on the bottom but part of it still pokes out the top, the body displaces a volume corresponding only to the fraction of the body that is submerged. Now, humans have a density very close to that of water. In fact, in a deep pool, humans can float or sink depending on how much air is in their lungs. But in a shallow tub, they cease to become buoyant once they support their weight on the bottom. Therefore, for a perpetrator seated or standing in a bathtub, translating the amount of water displaced into the total volume of the perpetrator (which, since a human's density is roughly that of water, gives the mass) requires knowing what fraction of his body was submerged.
Given the uncertainties involved, it is no mean feat for Charlie later in Scene 25 to compute a very precise net water displacement of 89.6 liters. On the other hand, it requires an outright dash of Hollywood magic to make the leap from water displacement to total volume of the perpetrator. Because both humans and water have densities of about one kilogram per liter and because one kilogram equals roughly 2.2 pounds, Charlie's computation corresponds to a perpetrator of at least 198 pounds, with a correction still needed to account for any unsubmerged portion. Colby apparently applies this correction when making the leap from 198 pounds to a a total perpetrator mass of 210-215 pounds. Using this figure, Charlie and Don are able to leverage Archimedes' principle (which is, after all a very appropriate thing to do, given that the great Greek mathematician is also known for his formulation of the "law of the lever") to once again get their man!
Evaporation
CHARLIE
And... the towel's edge is wet.
LARRY
We'll have to calculate for the
towel's absorption, evaporation,
the bubbles... but we know that at
some point, the water level was at
minimum, right here.
Evaporation is the process by which molecules of a liquid spontaneously become gaseous and escape from the bulk liquid without the liquid having been brought to its normal boiling temperature. The disappearance of puddles of water on pavement is due to evaporation, as is the drying of wet towels. Evaporation is therefore the opposite of condensation, in which molecules of a gas spontaneously become liquid. The basic theory of evaporation is a relatively straightforward application of thermodynamics involving concepts such as vapor pressure, enthalpy of vaporization, and Clapeyron's equation.
However, analyzing evaporation in practice is somewhat more complicated, and involves knowing or estimating of a wide variety of empirical factors. So while Charlie can certainly handle the mathematics of evaporation, solving the problem of the drying towel probably requires consultation with Larry, other physicists, or hydrologists. We'll say more about this in Scene 22.
(More) evaporation
LARRY
We should also account for some
evaporation... It's negligible,
very likely, but still...
CHARLIE
Evaporation... Right here.
Charlie points it out on the boards as Amita enters.
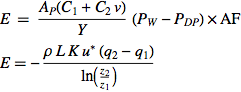
Charlie is lucky his computations don't sensitively depend on determining evaporation rates under non-laboratory conditions. Should he have been forced to do this, he would have had to consider semi-empirical formulas such as the ones above. In the first equation, which arises from studies of the evaporation rate in indoor swimming pools, E is the evaporation rate of water (in pounds per hour), AP is the area of the tub surface (in square feet), C1 is a constant given by 69.4 BTU/(h ft2) inHg, C2 is a constant given by 30.8 BTU/(h ft2) inHg, v is the air velocity over water surface (in miles per hour), Y is the latent heat required to change water vapor at surface water temperature (in BTU per pound), PW is the saturation vapor pressure taken at the surface water temperature (in inches of mercury), PDP is the saturation pressure at room air dew point (in inches of mercury), AF is an "activity factor" of order unity that takes into account the number of people in the water and the amount of their activity. Here, inHg means inches of mercury (normal atmospheric pressure is 29.92 inches of mercury, or 760 millimeters of mercury), and BTU is a British thermal unit (a unit of energy equal to about 1055 joules).
Similarly, the second equation comes from an application of an approximate hydrological technique known as the
"aerodynamic method," which requires taking measurements of temperature and vapor pressure at two heights
above the surface of a (large) body of water as well as measuring wind speed. In this formula, E is evaporation,
![]() is air density,
L is the latent heat of vaporization, K is von Kármán's constant, u* is the friction velocity, q2 - q1 is the specific humidity difference between the air and near the water surface,
z2 is the height at which the dew point
temperature measurement is taken, and z1 is a
height near the water surface. Specific humidities must then be computed using other empirical formulas based on
pressure and temperature.
is air density,
L is the latent heat of vaporization, K is von Kármán's constant, u* is the friction velocity, q2 - q1 is the specific humidity difference between the air and near the water surface,
z2 is the height at which the dew point
temperature measurement is taken, and z1 is a
height near the water surface. Specific humidities must then be computed using other empirical formulas based on
pressure and temperature.
So while Charlie and Larry might theoretically be able to compute detailed evaporation information based on the wet edge of a towel, doing this in practice would be very difficult. Fortunately, both Charlie and Larry have other mathematical and physical means at their disposal, and those prove sufficient for the task at hand.
Apollonian networks
LARRY
I did think some of the math was
a little subjective... your random
Apollonian Networks in particular.
The Greek geometer Apollonius of Perga (ca. 262-ca. 190 BC) was known as "The Great Geometer." He is perhaps best known for his monumental treatise on conic sections entitled On Conics. In this treatise, the term ellipse (see Episode 401 Math Notes) was first used. In addition, in his work Tangencies, Apollonius showed how to construct the circle that is tangent to three given circles--and more generally, how to construct the circle that is tangent to any three objects, where each object may be a point, line, or circle. This latter problem is today known as Apollonius' problem in his honor.
 |
Apollonius' name is also associated with a particular nested pattern of circles known as the Apollonian gasket. The Apollonius gasket is a fractal that can be constructed by beginning with three equal and mutually tangent circles, constructing the center circle that is externally tangent to each of them (this is known as the inner Soddy circle), then continuing the process by filling in circles in each of the remaining gaps that are mutually tangent to each group of three surrounding circles one step at a time. Several iterations of this process are illustrated at left. |

The Apollonian gasket can be generalized from the plane to a three-dimensional construction by beginning with four mutually tangent spheres instead of three mutually tangent circles. An Apollonian-like construction based on nesting spheres in three dimensions is shown at left. Sets of mutually tangent spheres have even more intricate properties than do tangent circles, including a remarkable result that every chain of tangent spheres satisfying certain tangency relationships closes into a "necklace" after six spheres, regardless of where the first sphere is placed. This beautiful result was demonstrated in 1937 by Nobel-Prize-winning English chemist Frederick Soddy in 1937, and the collection of spheres so arranged is known as Soddy's hexlet. Even more amazingly, it is a special case of a yet more general result known as Kollros' theorem. There are many other remarkable results involving nested tangent spheres, one of which is known as the bowl of integers.
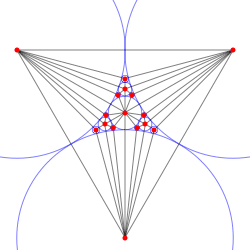
Connecting the centers of touching spheres in the above construction by edges gives a graph (see Episode 401 Math Notes) known as an Apollonian network. (Here, "network" is a type of directed or undirected graph that may have weights associated with its edges.) The process is illustrated at right for the case of the usual planar Apollonian gasket. Apollonian networks turn out to have some very special properties. In addition to being either deterministic or random, they are simultaneously scale-free, display small-world effects, can be embedded in a Euclidean lattice, and show space-filling as well as matching graph properties. These networks describe force chains in granular packings, fragmented porous media, hierarchical road systems, and area-covering electrical supply networks. Apollonian networks share many features of neuronal systems, and have been used to study the brain.
More friendship math
CHARLIE
I just know what I want to say now
about friendship. I know what goes
along with the math.
AMITA
I'm glad to hear it...
A beat. Charlie's focus returns to the computer, the
writing... Amita watches for a beat longer, then slowly
backs on out without disturbing him.
Charlie's study of friendship mathematics continues to go full steam (see Episode 401 Math Notes). While we have a number of interesting things to say on the subject, we're sure Charlie will give us other opportunities in future episodes, so we will once again defer additional mathematical discussion until a future Friday. Stay tuned!
References
American Society of Civil Engineers. Hydrology Handbook, 2nd ed. Reston, VA: ASCE Press, 1996.
Andrade, J. S. Jr.; Herrmann, H. J.; Andrade, R. F. S.; and da Silva, L. R. "Apollonian Networks: Simultaneously Scale-Free, Small World, Euclidean, Space Filling, and with Matching Graphs." Phys. Rev. Lett. 94, 018702-1-4, 2005.
Artmann, K. "Berechnung der Seitenversetzung des totalreflektierten Strahles." Ann. Phys. 2, 87-102, 1948.
Boyd, D. W. "The Residual Set Dimension of the Apollonian Packing." Mathematika 20, 170-174, 1973.
Brozovsky, L. and Petricek, V. "Recommender System for Online Dating Service." 9 Mar 2007. http://arxiv.org/abs/cs/0703042
Chauvat, D.; Emile, O.; Bretenaker, F.; and Le Floch, A. "Direct Measurement of the Wigner Delay Associated with the Goos-Hänchen Effect." Phys. Rev. Lett. 84, 71-74, 2000.
Fedorov, F. I. "K teorii polnogo otrazheniya." Dokl. Akad. Nauk SSSR 105, 465-468, 1955.
Goos, F. and Hänchen, H. "Ein neuer und fundamentaler Versuch zur Totalreflexion." Ann. Phys. (Leipzig) 1, 333-346, 1947.
Goos, F. and Lindberg-Hänchen, H. "Neumessung des Strahlversetzungseffektes bei Totalreflexion." Ann. Phys. (Leipzig) 5, 251-252, 1949.
Imbert, C. "Calculation and Experimental Proof of the Transverse Shift Induced by Total Internal Reflection of a Circularly Polarized Light Beam." Phys. Rev. D 5, 787-796, 1972.
Jones, R.; Smith, C.; and Löf, G. "Measurement and Analysis of Evaporation from an Inactive Outdoor Swimming Pool." Proceedings of the 1993 Annual Conference of the American Solar Energy Society. Washington D.C., April 1993.
Jones, R.; Smith, C.; and and Löf, G., "Measurement and Analysis of Evaporation from an Inactive Outdoor Swimming Pool." Solar Energy 53, 3, 1994.
Li, C.-F. "Unified Theory for Goos-Hänchen and Imbert-Fedorov Effects." Phys. Rev. A 76, 013811-1-6, 2007.
Li, C.-F.; Duan, T.; and Yang, X.-Y. "Giant Goos-Hänchen Displacement Enhanced by Dielectric Film in Frustrated Total Internal Reflection Configuration." J. Appl. Phys. 101, 013103-1-5, 2007.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, p. 172, 1983.
Pellegrini, G. L.; de Arcangelis, L.; Herrmann, H. J.; and Perrone-Capano, C. "Modelling the Brain as an Apollonian Network." Jan. 27, 2007. http://www.arxiv.org/abs/q-bio/0701045
Smith, C.; Jones, R.; and Löf, G. "Rates of Evaporation from Swimming Pools in Active Use." American Society of Heating, Refrigeration, and Air Conditioning Engineers Transactions 104, 514, 1998.
Trott, M. http://www.mathematicaguidebooks.org/downloads/N_1_06_Evaluated.nb