LIZ
          Seems like it's not just about the
          numbers.  The elements of the design
          are just as important.

This sparks Charlie, he studies the imagery, the nautilus
shell...

FLASH CHARLIE VISION

Spiralling numbers flowing out of the nautilus shell like
a vivid natural life force.

BACK TO CHARLIE

Fibonacci numbers have another, more direct relation to spirals. Consider a golden rectangle, a rectangle with side lengths equal to 1 and the golden ratio. Then successive points dividing a golden rectangle into squares lie on a special curve known as the logarithmic spiral, illustrated above. The logarithmic spiral was first studied by René Descartes in 1638 and by Jacob Bernoulli. Bernoulli was so fascinated by the spiral that he had one engraved on his tombstone (although the engraver did not draw it true to form) together with the words "eadem mutata resurgo" ("I shall arise the same though changed").

Fibonacci numbers

                    DON
          What is it, Charlie?

                    CHARLIE
          ...It's a Fibonacci sequence.  Which
          continues from this first grid here...

The Fibonacci numbers gives the number of pairs of rabbits n months after a single pair begins breeding (assuming each newly born bunny begins breeding when two months old), as first described by Leonardo of Pisa (also known as Fibonacci) in his book Liber Abaci. Before Fibonacci wrote his work, the Fibonacci numbers had already been discussed by Indian scholars such as Gopala (before 1135) and Hemachandra (ca. 1150) who had long been interested in rhythmic patterns that are formed from one-beat and two-beat notes or syllables.

The Fibonacci numbers appear in many areas of mathematics, and their role in botany is sometimes called Ludwig's law. A number of especially elegant identities involving the Fibonacci numbers are given below; for more information, see The Wolfram Functions Site or MathWorld.

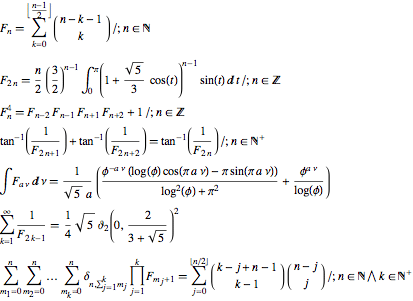
                    CHARLIE
          -- How? Numerology isn't math.
          It's just... nonsense.

Numerology

Numerology is the attempt to connect numbers and their properties with physical objects in the absence of an explanatory theory or framework. Since nature is in fact described extremely well by physical laws and mathematics, studies of numbers and their patterns can be a motivator for mathematics and scientific discovery. Pythagoras of Samos was a Greek philosopher and mathematician who founded the mystic Pythagorean cult, which was devoted to the study of numbers, seen by the Pythagoreans as concrete, material objects. For this reason, much of the work of the Pythagoreans is now regarded as numerology, even though Pythagoras and his followers supposedly made the proof that the square root of two , (a number now sometimes known as Pythagoras's constant), is irrational, i.e., cannot be expressed as a ratio of any two integers. Another example of numerological studies is Johannes Kepler's attempt to match the orbits of planets to nestings of the regular polyhedra with no explanatory theory or framework. However, careful study of the data led him to three laws of planetary motion--a very useful byproduct.

If numeric properties cannot be formulated into a theory that makes predictions about physical or mathematical objects but are stated to predict future events or seek connections with the occult, they are considered numerology instead of science. In fact, it is quite common for numbers to yield patterns that at first appear surprising, but actually have no fundamental significance. An excellent example comes from Martin Gardner, who wrote as follows in his classic work on pseudoscience.

"Consider the case of [German composer] Richard Wagner and the number 13. There are 13 letters in his name. He was born in 1813. Add the digits of this year and the sum is 13. He composed 13 great works of music. Tannhauser, his greatest work, was completed on April 13, 1845, and first performed on March 13, 1861. He finished Parsifal on January 13, 1882. Die Walkure was first performed in 1870 on June 26, and 26 is twice 13. Lohengrin was composed in 1848, but Wagner did not hear it played until 1861, exactly 13 years later. He died on February 13, 1883. Note that the first and last digits of this year also form 13. These are only a few of the many important 13's in Wagner's life."

There is a fair amount of numerology in the episode "Thirteen," specifically the common form of numerology related to finding hidden meaning in words and letters by assigning them numeric values. The title of this episode itself is a reference to the number 13, which is commonly associated with bad luck in Western culture. Such beliefs are so widespread that there is even a word (triskaidekaphobia) that specifically means "fear of the number 13." The association of bad luck with the number 13 has been attributed to the fact there were 13 people at the Last Supper of Jesus, although this association seems to have originated only in medieval times. The association has also been linked to that fact that lunisolar calendars (such as the Hebrew and Chinese calendars) must have 13 months in some years in order to synchronize the solar and lunar cycles, while the solar Gregorian calendar in universal current usage always has 12 months in a year, although several other explanations have also been put forward. This superstition leads some people to fear or avoid anything involving the number 13. In particular, this leads to interesting practices such as the numbering of floors as 1, 2, ..., 11, 12, 14, 15, omitting the number 13, in many high-rise American hotels, the numbering of streets avoiding 13th Avenue, and so on.

In general, summing a sequence of digits yields a result known as a digit sum. Digit sums have some interesting mathematical properties, including some beautiful relations to pi and the natural logarithm of 2. For more information on such sums, see MathWorld. We will discuss the numerology of letter sums shortly.

Summing digits associated with letters may also be the origin of the infamous number 666, the occult "number of the beast," also called the "sign of the devil" and associated in the Bible with the Antichrist. It has figured in many numerological studies, and is mentioned in Revelation 13:18: "Here is wisdom. Let him that hath understanding count the number of the beast: for it is the number of a man; and his number is 666." The origin of this number is not entirely clear, although it may be as simple as the number containing the concatenation of one symbol of each type (excluding M = 1000) in Roman numerals: DCLXVI = 500 + 100 + 50 + 10 + 5 + 1 = 666.

In general, unscientific methods can be investigated with scientific methods. The predictive power of mathematics is strong enough to forecast possible outcomes of meaningless, but rule-driven, processes. Mathematics as a science has a different epistemological status than physics, chemistry, biology, and so on because it does not a priori refer to the real world. One starts with a set of axioms and calculates "all possible" things. Some might not be possible or realizable in real life (on earth, in our particular universe). On the other hand, some might be possible but just don't happen to occur.

Mathematical beauty in nature and art

                    ALEX TROWBRIDGE
          You don't believe any of this, do you?

                    CHARLIE
          What, that numbers are spiritual and
          magical and mystical, no.  I'm a 
          mathematician.

                    ALEX TROWBRIDGE
          What about Fibonacci numbers, the Golden
          Ratio?

                    CHARLIE
          There is evidence that math occurs
          spontaneously in nature and in art.
          And I do acknowledge that there is 
          some mystery to that -- some beauty 
          to that...

A number of interesting and beautiful works that discuss the mathematics and form in nature include Sir Theodore Andrea Cook's The Curves of Life, Being an Account of Spiral Formations and Their Application to Growth in Nature, to Science and to Art, D'Arcy Wentworth Thompson's On Growth and Form, and Stephen Wolfram's A New Kind of Science.

Gematria

                    ALEX TROWBRIDGE
          It's called a "gematria" (geh-MAY-
          tria).  People into numerology look
          for meaning in such "digit-sums."

                    CHARLIE
          -- Of course they do.

Gematria is the application of numerology to the 22 letters of the Hebrew alphabet. It has been used by its proponents to derive alleged meaning and relationships between objects mentioned in holy texts. Although gematria is primarily applied only to the Hebrew alphabet, there is also a version of gematria dating from the early Middle Ages that applies to languages written using Latin characters. The following table gives the values normally assigned to the various Hebrew characters.

For example, consider the Name of God YHVW (Yahweh, meaning "I Am Who I Am"), illustrated below as written in Phoenician (1100 BC to AD 300), Aramaic (10th Century BC to 0) and modern Hebrew scripts. Using the above gematria table to assign values to the Hebrew characters yodh he waw he (read right to left) then gives a gematria value of 10 + 5 + 6 + 5 = 26.

Gematria has been used to analyze the text of Kings 7:23, which literally implies that the value of pi is 3 rather than 3.14159..., to obtain a more accurate value of 3.141507--which is within 0.003% of the true value of pi.

Greek numerology

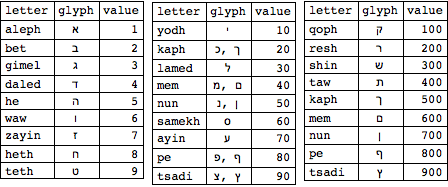
A Greek version of gematria uses the following table of values for translating words into numbers.

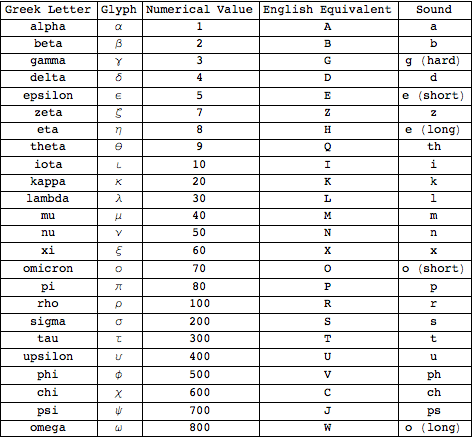
                    ALEX TROWBRIDGE
          So, the number 888 is associated with
          Christ, arrived at by adding up the
          numerical values of the Greek
          alphabet letters that spell "Jesus" --

She writes the letters on a clear board: I-H-S-O-U-S --

                    ALEX TROWBRIDGE (cont'd)
          ...I-H-S-O-U-S... and their numeric
          equivalents...
              (writes under the letters)
          ...10-8-200-70-400-200...

                    AMITA
          ...Which adds up to 888.

Using this table, we can see that in Greek gematria, the value associated with Jesus, which is transliterated as IHSOUS in Greek, is indeed 10 + 8 + 200 + 70 + 400 + 200 = 888, as mentioned by Alex Trowbridge.

Strong law of small numbers

Charlie counters Alex Trowbridge's comments by referring to the strong law of small numbers. The first strong law of small numbers states, "There aren't enough small numbers to meet the many demands made of them." The second strong law of small numbers states that, "When two numbers look equal, it ain't necessarily so." For example, Richard Guy noted the curious fact that for integers n = 0, 1, 2, ..., the function where is the ceiling function gives the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... (i.e., the first few Fibonacci numbers), but it subsequently continues with 91, 149, ..., which are not Fibonacci numbers.

Binary

                    CHARLIE
          If there's a pattern in these last
          four number grids, I don't see it.

                    LARRY
          The repetition of 0's and 1's could
          be some form of binary encoding.

Binary is the base-2 method of counting in which only the digits 0 and 1 are used. For example, in binary, the number 1011 represents 11, since . This base is used in computers, since all numbers can be simply represented as a string of electrically pulsed ons and offs. In computer parlance, one binary digit is called a bit, two digits are called a crumb, four digits are called a nibble, and eight digits are called a byte.

#	binary	#	binary	#	binary
1	1	11	1011	21	10101
2	10	12	1100	22	10110
3	11	13	1101	23	10111
4	100	14	1110	24	11000
5	101	15	1111	25	11001
6	110	16	10000	26	11010
7	111	17	10001	27	11011
8	1000	18	10010	28	11100
9	1001	19	10011	29	11101
10	1010	20	10100	30	11110

Consider the cumulative digit sum of all binary numbers up to 1, 2, ..., n. This sequence is monotone increasing (left figure below), but if the main asymptotic term is removed, we get a sequence of humped curves (right figure) tending towards a beautiful recursive function known as the Blancmange function.

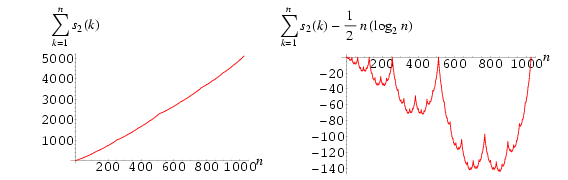
And that's all the math behind NUMB3RS for this week.

References

Cook, T. A. The Curves of Life, Being an Account of Spiral Formations and Their Application to Growth in Nature, to Science and to Art. New York: Dover, 1979.

Coxeter, H. S. M. "The Golden Section, Phyllotaxis, and Wythoff's Game." Scripta Mathematica 19, 135-143, 1953.

Coxeter, H. S. M. "The Role of Intermediate Convergents in Tait's Explanation for Phyllotaxis." J. Algebra 10, 167-175, 1972.

Dixon, R. "The Mathematics and Computer Graphics of Spirals in Plants." Leonardo 16, 86-90, 1983.

Dudley, U. Numerology, or, What Pythagoras Wrought. Washington, DC: Math. Assoc. Amer., 1997.

Gardner, M. Fads and Fallacies in the Name of Science. New York: Dover, 1957.

Gardner, M. "Mathematical Games: Patterns in Primes are a Clue to the Strong Law of Small Numbers." Sci. Amer. 243, 18-28, Dec. 1980.

Guy, R. K. "The Strong Law of Small Numbers." Amer. Math. Monthly 95, 697-712, 1988.

Guy, R. K. "Graphs and the Strong Law of Small Numbers." In Graph Theory, Combinatorics, and Applications, Vol. 2 (Kalamazoo, MI, 1988). New York: Wiley, pp. 597-614, 1991.

Guy, R. K. "The Second Strong Law of Small Numbers." Math. Mag. 63, 3-20, 1990.

Parsons, J. "Overview of Hebrew Gematria." http://hebrew4christians.com/Grammar/Unit_Eight/Hebrew_Gematria/hebrew_gematria.htm

Thompson, D. W. On Growth and Form. Cambridge, England: Cambridge University Press, 1952.

Timothy Ministries. "Dictionary of Theology: YHVH." http://timothyministries.org/theologicaldictionary/references.aspx?theword=YHVH

Triune-Being Research Organization Ltd. "In Search of the Beast 666." http://www.triune-being.com/Numerology/names/name666.htm"

Vogel, H. "A Better Way to Construct the Sunflower Head." Math. Biosci. 44, 179-189, 1979.

Wikipedia. Gematria and Numerology

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, 2002.