
LIZ
Seems like it's not just about the
numbers. The elements of the design
are just as important.
This sparks Charlie, he studies the imagery, the nautilus
shell...
FLASH CHARLIE VISION
Spiralling numbers flowing out of the nautilus shell like
a vivid natural life force.
BACK TO CHARLIE
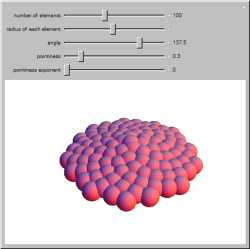
In almost all above-ground growth in plants, new sprouts come out at angles of about 137.5° relative to the previous
one. But between each sprout, the main stem or trunk has grown different amounts. The arrangement of leaves and petals
in plants is known as
phyllotaxis. Use this
Demonstration to see the effect this has on overall form.
DON
What is it, Charlie?
CHARLIE
...It's a Fibonacci sequence. Which
continues from this first grid here...
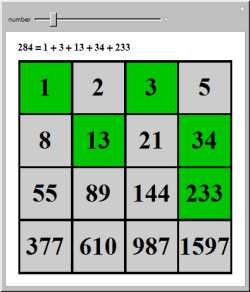
DON
The sequence continues, right?
CHARLIE
Yeah.
DON
So, if there was another grid after
this one --
CHARLIE
-- The next missing number series
could be our next victim.
Charlie grabs David's pad, scribbles. Holds it up. Another
7-digit number.
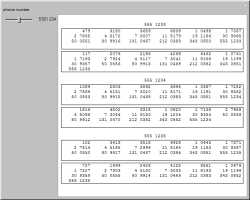
The
Fibonacci sequence, 1, 1, 2, 3, 5,
8,..., is obtained by adding the two previous terms to get the next term. By starting with different initial terms, any
number can eventually be reached. In this Demonstration, manually chosen phone numbers result at the ends of two
different sequences.
ALEX TROWBRIDGE
What about Fibonacci numbers, the Golden
Ratio?
CHARLIE
There is evidence that math occurs
spontaneously in nature and in art.
And I do acknowledge that there is
some mystery to that -- some beauty
to that...
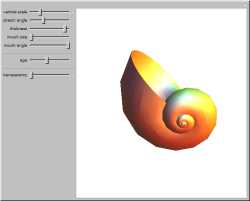
A simple model for the growth of mollusk
shells. In each case new shell material is progressively added at the open end of the shell. The
sliders control the amount of material added at each stage at different points around the opening; the line from the
center indicates the progressive lateral displacement of the opening. All shells produced by adding material according
to fixed rules of the kind shown here have the property that throughout their growth they maintain the same overall
shape.
ALEX TROWBRIDGE
It's called a "gematria" (geh-MAY-
tria). People into numerology look
for meaning in such "digit-sums."
CHARLIE
-- Of course they do.

A frequent
numerology exercise involves
turning letters into numbers (
a = 1,
b = 2, ...,
z = 26), then summing the values (
i.e.,
computing their
digits sums). This
Demonstration lets you see what words have specific sums.
A coin-sorting machine. A BUCKET OF COINS tossed in, as we --
AMITA (V.O.)
Imagine dumping in a bucket-full of
coins -- not just U.S. coins, but
currencies from around the world --
thousands of different coins...
PUSH IN AND DISSOLVE "into" the machine, its inner workings.
The COINS swirl around on a circular tray with different-
sized sorting holes. EQUATIONS VECTOR-ROTATE WITH THE COINS.
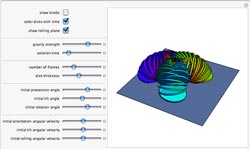
This Demonstration shows snapshots of a disk rolling on a plane. For the calculation, it is assumed that the disk has
infinitesimal thickness, rolls without friction, and does not slide or slip. A rolling disk is one of the simplest
examples of a
nonholonomic system. It
is completely
integrable, and as a result,
the sequence of snapshots form
nonchaotic
sequences exhibiting a certain symmetry.
CHARLIE
If there's a pattern in these last
four number grids, I don't see it.
LARRY
The repetition of 0's and 1's could
be some form of binary encoding.

The pattern formed by the
binary digits is ultimately nested.







