
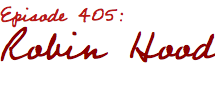

CHARLIE
Check out these acetone smears.
It's perfect for a Hand Path
Prediction.
AMITA
(excited)
With an adaptation of Listing's
Law, right?
Listing's law
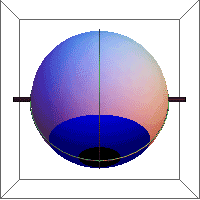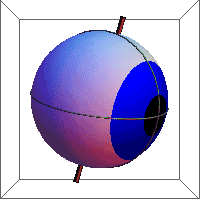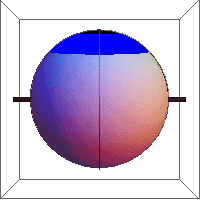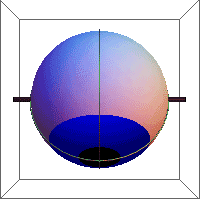
Listing's law is the observed phenomenon that when the eye turns from looking at one object and fixes upon another, it revolves about an axis orthogonal to a plane cutting both the former and the present lines of vision. Mathematically, this means that the space of all eye rotations is a subgroup of the special orthogonal group SO(3) of all proper rotations (i.e., not improper rotations) in Euclidean 3-space.
There is also a phenomenon that the body and eyes move before an action actually happens, which is related to Listing's law but does not actually seem related to hand path motions.
Projectile motion
CHARLIE
It's no different from a golf
swing, really...
ENTER AUDIENCE VISION
A golfer, Bobby Jones re-incarnated on the tee box.
CHARLIE (V.O.) (cont'd)
By watching and analyzing the swing
you can tell from the point of
impact exactly where the golf ball
will end up...
The trajectory of the ball is highlighted...
CHARLIE (V.O.) (cont'd)
Without ever looking at the
fairway. Now imagine the golfer is
invisible...
Bobby Jones vanishes. Club and ball are still there.
CHARLIE (V.O.) (cont'd)
By looking at the motion of the
club as well as the point of impact you
could reconstruct how the golfer
was positioned.
We discussed the mechanics and kinematics of traffic accidents in Episode 402, Velocity. While the modeling of automobile accidents can be quite complicated, the motion of simple projectiles such as golf balls is much more straightforward.
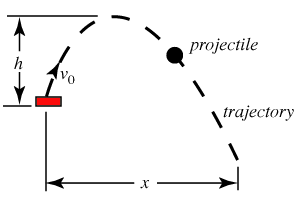
A projectile is an object that is propelled (or thrown) with some initial velocity and then allowed to be acted upon by the forces of gravity and possibly drag. The maximum upward distance h reached by a projectile is called the height, the horizontal distance x traveled is called the range, and the path of the object is called its trajectory. The study of the motion of projectiles is called ballistics.
To simplify the ballistic problem, consider an approximate model in which air drag is insignificant, there is no wind, etc.
(Considering the full case is a bit more complicated. For example, in the particular case of golf balls, the dimples
actually cause golf balls to travel further than smooth balls because they delay the separation of the boundary layer of
air around the ball. For more details, see Jearl Walker's entertaining and informative book The Flying Circus of
Physics.) For a projectile launched with a speed v at
an angle ![]() to the horizontal, the range is given by
to the horizontal, the range is given by
![]()
where t is the time in motion. On a level plane where the projectile lands at the same altitude as it was launched, a derivative of the maximum height shows that it is reached after a time
![]()
where g is the acceleration due to gravity. The range is then the distance traveled in time ![]() (
(![]() up and
up and ![]() down),
down),
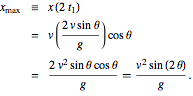
Because of the ![]() in the argument of the sine function, it follows that
in the argument of the sine function, it follows that
![]()
so equal ranges are achieved by complementary angles. Therefore, on a level plane, the maximum range occurs when the derivative vanishes,
![]()
![]()
or ![]() .
.
However, the above does not hold if the initial and final altitudes are different. If the altitude of the landing point
is Δh higher than that of the launch point, then the time required for the downward portion of the fall
![]() is given by
is given by
![]()
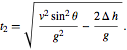
The distance traveled in the time required for both the downward and upward trips is then
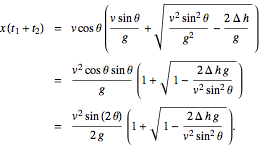
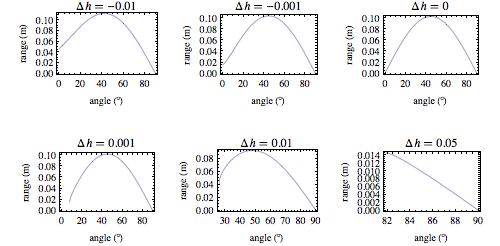
Ranges computed using this formula are shown below for g = 9.81 m/s2, v = 1 m/s, and Δh = -0.01, -0.001, 0, 0.001, 0.01, and 0.05.
The mathematics of love (again)
LARRY
The noticeable absence of a certain
combinatorics professor makes me
think your own affairs of the heart
have heightened your empathy.
CHARLIE
Love is one puzzle after another.
LARRY
In quantum experiments, when we
change our minds, we change the
state of matter itself. Imagine,
how deeply our thoughts can affect
our relationships.
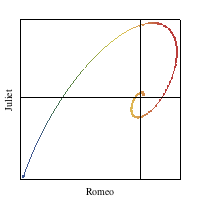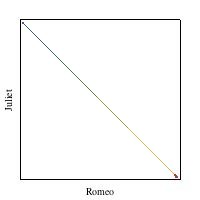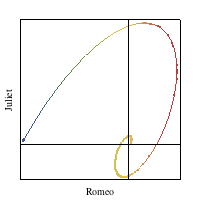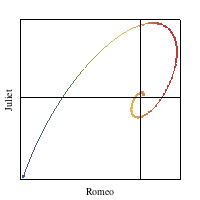
We previously discussed the mathematical modeling of affection in Episode 402, Velocity. The animation at right (and the linked Demonstration) solved a set of coupled differential equations that describe one possible dynamical model on how love varies over time. Time is indicated by color and runs from red to blue in the figure.
The Nobel Prize of mathematics
AMITA
Thanks... maybe we'll wait until
you win your Fields Medal.
Charlie moves to her. She smiles.
CHARLIE
You really think I'm going to win a
Fields?
AMITA
Why do you think I'm with you?
CHARLIE
Thought it was for my hair.
AMITA
Well, that, too.
The Fields Medals are commonly regarded as mathematics' closest analog to the Nobel Prize (which does not exist for mathematics), and are awarded every four years by the International Mathematical Union to one or more outstanding researchers. "Fields Medals" are more properly known by their official name, "International medals for outstanding discoveries in mathematics."
The Field Medals were first proposed at the 1924 International Congress of Mathematicians in Toronto, where a resolution was adopted stating that at each subsequent conference, two gold medals should be awarded to recognize outstanding mathematical achievement. Professor J. C. Fields, a Canadian mathematician who was secretary of the 1924 Congress, later donated funds establishing the medals, which were named in his honor. Consistent with Fields's wish that the awards recognize both existing work and the promise of future achievement, it was agreed to restrict the medals to mathematicians not over forty at the year of the Congress. In 1966 it was agreed that, in light of the great expansion of mathematical research, up to four medals could be awarded at each Congress.


Fields Medal front and back views.
© Fields Institute
The Fields Medal carries with it a prize of Canadian $15000. The first Fields Medals were awarded in 1936 at the World Congress in Oslo. The Fields Medal is made of gold, and shows the head of Archimedes (287-212 BC) together with a quotation attributed to him: "Transire suum pectus mundoque potiri" ("Rise above oneself and grasp the world"). The reverse side bears the inscription: "Congregati ex toto orbe mathematici ob scripta insignia tribuere" ("The mathematicians assembled here from all over the world pay tribute for outstanding work").
Nobel prizes were created in the will of the Swedish chemist and inventor of dynamite Alfred Nobel, but Nobel, who was an inventor and industrialist, did not create a prize in mathematics because he was not particularly interested in mathematics or theoretical science. In fact, his will speaks of prizes for those "inventions or discoveries" of greatest practical benefit to mankind. While it is commonly stated that Nobel decided against a Nobel prize in math because of anger over the romantic attentions of a famous mathematician (often claimed to be Gosta Mittag-Leffler) to a woman in his life, there is no historical evidence to support the story.
See MathWorld for a list of past Fields medal recipients, the most recent of whom were honored at the 2006 International Congress of Mathematicians in Madrid, Spain.
On-line dating math
CHARLIE
Think about an on-line dating
service.
WALKER
Now Professor, what makes you think
I'd be familiar with that concept?
CHARLIE
Hypothetically.
AUDIENCE VISION
Questionnaire with a list of questions on the left, scale 1-5
on the right.
CHARLIE (V.O.) (cont'd)
You fill out a detailed personality
profile... gender, height,
education...
Users of online dating services must discover, collate, and act upon large amounts of information in their search for a suitable romantic partner. Many different techniques have been developed in an attempt to automate the search process and provide the best possible matching criteria. However, as discussed by Lukas Brozovsky and Vaclav Petricek, there is a surprising lack of work published in this area.
Matchmaking is commonly cited as a prototypical application of recommender systems. A recommender system is a specific type of information-filtering technique that attempts to present information of likely of interest to the user. Recommender systems have been popularized by commercial organizations such as Amazon (for books) and Netflix (for movies).
The most widely used recommender systems are based on a set of algorithms known as collaborative filtering. There are two classes of collaborative filtering algorithms: memory-based and model-based. Memory-based systems require the whole rating matrix to be stored in memory. A typical example of a memory-based algorithm is the k-nearest neighbor algorithm. Model-based algorithms include methods based on the mathematical decomposition (by techniques such as singular value decomposition) of matrices that encode rating informationn. It is therefore not surprising that collaborative filtering research is an extremely active field. It is also not unexpected that it is mathematically very challenging.
References
Brozovsky, L. and Petricek, V. "Recommender System for Online Dating Service." 9 Mar 2007. http://arxiv.org/abs/cs/0703042
Fields Institute. "The Fields Medal." http://www.fields.utoronto.ca/aboutus/jcfields/fields_medal.html
Hepp, K. "On Listing's Law." Comm. Math. Phys. 132, 285-292, 1990.
Polpitiya, A. D.; Dayawansa, W. P.; Martin C. F.; and Ghosh, B. K. "Geometry and Control of Human Eye Movements." IEEE Trans. Autom. Control 52, 170-180, 2007.
Rosales, R.; Athitsos, V.; Sigal, L.; and Sclaroff, S. "3D Hand Pose Reconstruction Using Specialized Mappings." In Computer Vision, 2001. ICCV 2001. Proceedings. Eighth IEEE International Conference on Computer Vision (ICCV). Vancouver, BC, Canada, pp. 378-385, 2001. http://www.cs.bu.edu/techreports/pdf/2000-022-hand-pose-estimation-with-sma.pdf
Sprott, J. C. "Dynamical Models of Love." Nonlin. Dyn., Psych., Life Sci. 8, 303-313, 2004. http://sprott.physics.wisc.edu/pubs/paper277.pdf
Sprott, J. C. "Dynamical Models of Happiness." Nonlin. Dyn., Psych., Life Sci. 9, 23-36, 2005. http://sprott.physics.wisc.edu/pubs/paper281.pdf
Walker, J. "Dimpled Golf Balls." § 4.96 in The Flying Circus of Physics with Answers. New York: Wiley, pp. 102 and 262, 1977.