Charlie snatches the box, removes the book, gently,
cautiously weighing it.  He holds it up, studying the cover.

                    DON
          Nice picture.

We see a dapper PHOTO of Charlie on the back cover.

So what exactly is an icosidodecahedron, and how does one stellate it? Before answering these questions (although readers can quickly discover the answers by clicking the links above), let us first give some background information on polyhedra.

A polyhedron--a word deriving from the Greek poly (many) and the Indo-European hedron (seat)--is a three-dimensional solid bounded by polygonal faces that are joined at their edges. If there are no "dimples," so that every pair of points in the interior of the polyhedron is connected by a line that lies entirely inside the polyhedron, the solid is called a convex polyhedron.

The Platonic solids, also called the regular solids or regular polyhedra, are among the simplest polyhedra. They are polyhedra with equivalent faces composed of congruent convex regular polygons. (Here, the requirement that the faces be convex exlcudes the possibility of faces composed of "regular" polygons, like the pentagram, that lead to another class of fascinating polyhedra known as the Kepler-Poinsot solids, which we do not, unfortunately, have time to discuss in detail.)

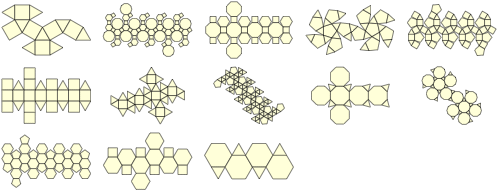
As proved by Euclid in the last proposition of the Elements, there are exactly five Platonic solids: the cube, dodecahedron, icosahedron, octahedron, and tetrahedron, illustrated above both as solids and in flattened out ("net") form. The Platonic solids were known to the ancient Greeks, and were described by Plato in his Timaeus ca. 350 BC. In this work, Plato equated the tetrahedron with the element fire, the cube with earth, the icosahedron with water, the octahedron with air, and the dodecahedron with the stuff of which the constellations and heavens were made. Predating Plato, the neolithic people of Scotland developed the five solids a thousand years earlier. The stone models are kept in the Ashmolean Museum in Oxford.

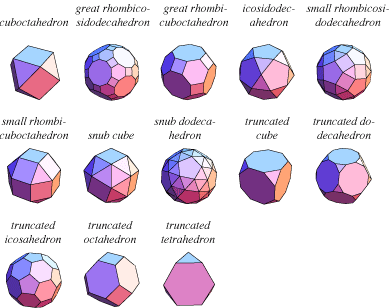
The thirteen Archimedean solids, sometimes also referred to as the semiregular polyhedra, are the next most symmetric class of polyhedral solids. They are the convex polyhedra that have a similar arrangement of nonintersecting, regular convex polygons of two or more different types arranged in the same way about each vertex, with all sides the same length.

The Archimedean solids are distinguished by having very high symmetry, thus excluding solids belonging to the so-called dihedral group of symmetries (e.g., the two infinite families of regular prisms and antiprisms). The aforementioned icosidodecahedron is in fact an Archimedean solid because it consists of 20 equilateral triangular faces and 12 regular pentagonal faces.

Stellation is the process of constructing polyhedra by extending the facial planes past the polyhedron edges of a given polyhedron until they intersect. The set of all possible polyhedron edges of the stellations can be obtained by finding all intersections on the facial planes. Since the number and variety of intersections can become unmanageable for complicated polyhedra, additional rules are sometimes added to constrain allowable stellations. Some solids (such as the cube and tetrahedron) have no stellations, some (such as the dodecahedron and rhombic dodecahedron) have a small number, and some (such as the icosahedron and especially the rhombic triacontahedron) have many. Archimedean stellations have received much less attention than Platonic stellations, but the stellation of the icosidodecahedron is clearly an attractive one.

Some stellations can be visualized through cumulation, which is the process of replacing the faces of a polyhedron with pyramids of height h (where h may be positive, zero, or negative) and using the faces as the base. The cumulation of the icosidodecahedron is illustrated below, on the right, right and in the animation above.

Stellating an icosidodecahedron and beveling the edges gives a particular beautiful geometric object, as illustrated above. And once this object has been created on a computer (in this case using Mathematica), it is even possible to turn the virtual object into a real, tactile one using a relatively new technology known as three-dimensional printing. For more details on the process by which the stellated icosidodecahedron was turned into the solid model featured on NUMB3RS and the back cover of Charlie's new book (right figure below), see Joshua Martell's Wolfram Blog post on the subject.

Escape radius

Charlie enters, sees Don.

                    CHARLIE
          Hey.  What's up?

                    DON
          There was a murder last night in Van
          Nuys and I'm hoping you can do that
          thing with the radius.

                    CHARLIE
          An escape radius?  Don, after this
          many hours, calculating the max
          travel distance won't give us --

                    DON
          I need something.

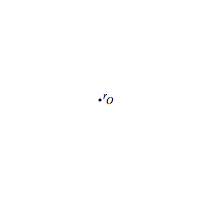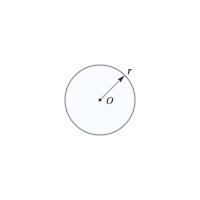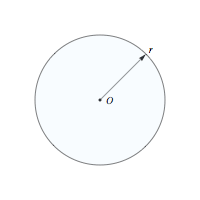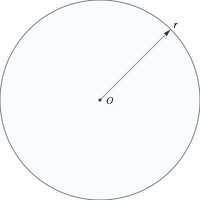
In Episode 323, "Money for Nothing," thieves stole a truck containing a large vault. Charlie developed "escape math" to determine where the vault might be. The start of Episode 221, "Rampage," also used the concept of the escape radius. If a fugitive begins at a known location O (the origin) at a known time and has a fixed maximum speed of travel v, then after a time t, the fugitive must be located within a circle of radius r = v t centered at O. As time increases, the size of the circle clearly increases.

As Charlie correctly points out in this episode, the escape radius isn't a useful bounding technique unless the fugitive's mode of transportation is known and the elapsed time is not too great.

CART analysis

Charlie notices a huge Oak hanging over the yard.

FLASH CHARLIE VISION

The tree shifts from reality to black and white as words and
numbers strike the limbs with precision, pruning it.

BACK TO CHARLIE

                    CHARLIE
          What about a classification and
          regression tree?

                    LARRY
              (good idea)
          "CART" Analysis might uncover where
          he went wrong...

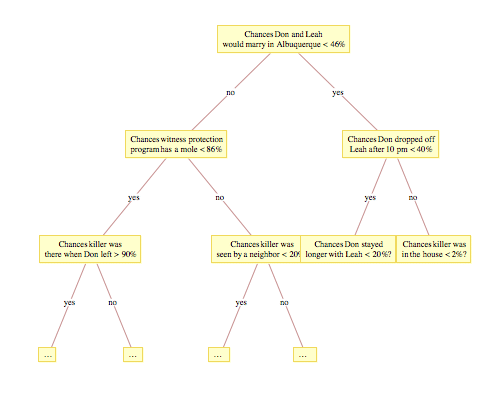
A decision tree (also known as a tree diagram) is a tool intended to assist decision making that uses a graph to analyze possible decisions and their consequences. There are three main kinds of decision trees:

• Classification tree analysis refers to the case in which the predicted outcome is the class to which the data belongs.
• Regression tree analysis refers to the case where the predicted outcome can be considered to be a real number.
• CART (Classification and Regression Tree) analysis, a term first introduced by Breiman et al. in 1984, refers to both aforementioned procedures.

Don ends the scene by asking Charlie if he can connect McGurn and Gibbs. A possible tree diagram for this decision is illustrated below. When carrying out the CART analysis, it is important to take into account that Don's actions are a mixture of rational and irrational decisions.

Goal theory, path analysis, and mazes

AUDIENCE VISION

A Rat travels through a maze.

                     CHARLIE (V.O.) (cont'd)
          Like a rat in a maze, we have a set
          of known variables.  We know the rat
          wants to escape the maze.

We see the exit.

                     CHARLIE (V.O.) (cont'd)
          The rat has other needs and desires;
          food, cheese, water, a mate.

We see cheese, water and another rat in succession.

                     CHARLIE (V.O.) (cont'd)
          All of these factor into approaching
          a desirable outcome.

The Rat exits the maze into a student's hands to be stroked.

Goal theory is the educational psychology term that referrs to research into learning motivation.

In statistics, path analysis is a type of multiple regression analysis and refers to the analysis of causal models when single indicators are employed for each model variable.

A maze is a set of possible paths and obstacles that must be navigated before reaching a goal. Normally, the obstacles are impermeable walls, and the goal of the maze is to start at one given point and find a path through the passages that reaches a second given point.

The above pattern (in either its square or rounded form) has appeared with remarkably little variation in a large variety of places throughout history: Cretan coins, graffiti at Pompeii, the floor of the cathedral at Chartres, carvings in Peru, and logos for aboriginal tribes. For approximately three thousand years, it has been the single most common design used for labyrinths.

Episode 311, "Killer Chat," included a fractal maze on one of Charlie's chalkboards (left figure below). Episode 317, "One Hour," discussed a particular type of maze known as a state diagram (right figure below).

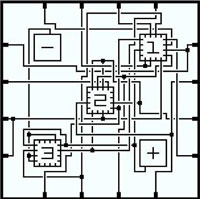
Figure-ground illusions

Larry draws a simple profile looking to the right.

                     LARRY (cont'd)
          A woman in profile...

Then draws a second profile facing the first.

                     LARRY (cont'd)
          Facing another woman, also in
          profile.

Now he shades the center.

                     LARRY (cont'd)
          But when I shade the center --

Larry shows his profiles can also now be seen as a vase.

                     CHARLIE
          It becomes a vase.

Researchers have proposed that, for the purpose of recognition, human vision parses shapes into component parts. However, as noted by Singh, Seyranian, and Hoffman, precisely how is not yet known.

The goblet illusion is an optical illusion in which the eye alternately sees two black faces, or a white goblet. This kind of ambiguous illusion is called figure-ground reversal, a term that refers to the perceptual separation of visual elements based on contrast. The principle of figure-ground is fundamental for psychologists who study perception. Depending on whether the white or black color is seen as the figure (foreground) or the ground (background), the brain interprets the picture as two different images. Furthermore, it is difficult for many people to perceive both figure and ground simultaneously.

Further examples of figure-ground illusions are the "rabbit-duck" and "young girl-old woman" illusions, illustrated below.

Steganography

                     YAEGGER
               (catching on)
           ...Gangs in Pelican Bay have been
           encoding messages in jailhouse
           artwork for years.

                     CHARLIE
           Street steganography.
               (to Liz)
           May I?

Steganography is the art, method, practice, and study of hiding secret messages inside other messages, for example, within images that appear to be innocent. Stegranography has played a role in previous episodes of NUMB3RS. In Episode 208, "In Plain Sight," Charlie helped track down a fugitive by finding a hidden pornographic picture concealed in a commonplace picture, and also by detecting a hidden hard drive partition. In Episode 305, "The Mole," Charlie asserted that the NSA discovered that some terrorist groups hide messages in digital images using steganography.

To see how easy it is to conceal hidden messages in images using steganography, even without any sophisticated image processing, consider the above example from Wikipedia. Import the above left image from Wikipedia. This can be done, for example, in Mathematica using the command

image = Import[ "http://upload.wikimedia.org/wikipedia/en/4/4e/StenographyOriginal.png"]

(left image). This is a Portable Network Graphics (PNG) file containing eight bits of data (where a bit is a 0 or 1 in the binary number system) in each of the three RGB (red, green, blue) color channels. Now replace the last two bits of each color channel with 0s, giving the middle image. This can be done in Mathematica using

image2 = Graphics[Raster[image[[1, 1]] /. n_Integer :> FromDigits[ReplacePart[IntegerDigits[n, 2, 8], {7 -> 0, 8 -> 0}], 2], {{0, 0}, {200, 200}}, {0, 255}, ColorFunction -> RGBColor], ImageSize -> {200, 200}]

As can be seen in the middle image, there is no perceptible difference from the original when these "lowest-order bits" are removed. However, those bits do contain information. When you extract the last two bits from the original image,

image3 = Graphics[Raster[image[[1, 1]] /. n_Integer :> FromDigits[IntegerDigits[n, 2, 2], 2], {{0, 0}, {200, 200}}, {0, 3}, ColorFunction -> RGBColor], ImageSize -> {200, 200}]

and redisplay, you find that the tree is hiding a (Cheshire? ;) cat (right-hand image above). The lesson is that you can encode a lot of information in a 200 by 200 array of 2-bit triples.

Image cleaning

                     CHARLIE
           I can use a simple Morphological
           Image Cleaning Algorithm to find the
           hidden message.

                     CHARLIE (cont'd)
           The algorithm was originally intended
           to save corrupted images, but it's
           also useful to smooth out the grayscale
           image, removing the camouflage
           while revealing the thin features
           where a hidden message resides.

                     DON
           How long will it take?

                     CHARLIE
           Get a cup of coffee.

Mathematically, a linearly degraded (blurred) image is the convolution of the pristine image with a kernel function with additive noise. The problem is to find a best estimate of the pristine image from the noisy blurred data when the noise function is unknown. Deconvolution solves the inverse problem

given g and h, where ε is the noise and * denotes convolution, and is therefore an extremely important problem in many areas of mathematics, engineering, and science.

Deconvolution is ill-posed and will usually not have a unique solution even in the absence of noise. Linear deconvolution algorithms include inverse filtering and Wiener filtering. Nonlinear algorithms include the CLEAN algorithm, maximum entropy method, and LUCY. "Morphological image cleaning" is another published image-cleaning algorithm that preserves thin features while removing noise. It is claimed to be useful for cleaning grayscale images corrupted by dense, low-amplitude, random, or patterned noise. Note however that this image-cleaning algorithm seems to be intended for noise reduction, which is different from the application cited by Charlie.

These prominent image-cleaning algorithms are summarized below.

• CLEAN is an iterative algorithm that deconvolves a sampling function (known as the "dirty beam") from an observed brightness ("dirty map") of a radio source. This algorithm is fundamentally important to radio astronomy, where it is used to create images of astronomical sources that are observed using arrays of radio telescopes ("synthesis imaging"). As a result of the algorithm's importance to synthesis imaging, a great deal of effort has gone into optimizing and adjusting the algorithm. CLEAN is by necessity a nonlinear algorithm, since linear deconvolution algorithms are inapplicable to invisible distributions (i.e., incomplete sampling of the spatial frequency plane) such as maps obtained in synthesis imaging.
• Maximum entropy is a deconvolution algorithm (sometimes abbreviated MEM) that functions by minimizing a smoothness function ("entropy") in an image. Maximum entropy is also called the all-poles model or autoregressive model. For images with more than a million pixels, maximum entropy is faster than the CLEAN algorithm. MEM is commonly employed in astronomical synthesis imaging. In this application, the resolution depends on the signal-to-noise ratio, which must be specified. Therefore, resolution is image-dependent and varies across the map. MEM is also biased, since the ensemble average of the estimated noise is nonzero. However, this bias is much smaller than the noise for pixels with a SNR >> 1. It can yield super-resolution, which can usually be trusted to an order of magnitude in solid angle.
• LUCY is a nonlinear deconvolution technique that was used in deconvolving images from the Hubble Space Telescope before corrective optics were installed.

References

Breiman, L.; Friedman, J.; Olshen, R. A.; and Stone, C. J. Classification and Regression Trees. Wadsworth, 1984.

Martell, J. "3D Printing with Mathematica." http://blog.wolfram.com/2007/07/3d_printing_with_mathematica.html

Peters, R. A. "A New Algorithm for Image Noise Reduction using Mathematical Morphology." IEEE Trans. Image Proc. 4, 554-568, 1995. http://www.vuse.vanderbilt.edu/~rap2/papers/nreduce.pdf

Pullen, W. D. "Daedalus on Numb3rs." http://www.astrolog.org/labyrnth/daedalus/numb3rs.htm

Singh, M.; Seyranian, G. F.; and Hoffman, D. D. "Parsing Silhouettes: The Short-Cut Rule." Perception and Psychophysics 61, 636-660, 1999.

Wikipedia. Decision_tree_learning, Goal_Theory, Path_analysis_(statistics), Steganography

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, 2002.