Charlie enters, sees Don.
CHARLIE
Hey. What's up?
DON
There was a murder last night in Van
Nuys and I'm hoping you can do that
thing with the radius.
CHARLIE
An escape radius? Don, after this
many hours, calculating the max
travel distance won't give us --
DON
I need something.
As a
radius increases, the search space increases
by the radius squared. This Demonstration of the planets illustrates just how much larger an object can become with an
increase in radius.
LARRY
I'm starting to suspect that I can no
more live within the norms of their
singular convention than light can
escape the event horizon of a black
hole.
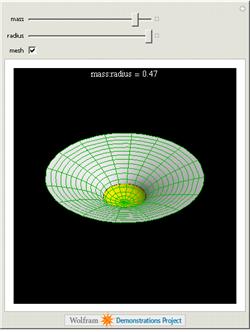
This Demonstration shows a two-dimensional analog of four-dimensional spacetime
curvature. This curvature is most
extreme around black holes.
AUDIENCE VISION
A Rat travels through a maze.
CHARLIE (V.O.) (cont'd)
Like a rat in a maze, we have a set
of known variables. We know the rat
wants to escape the maze.
Create a customized
maze.
CHARLIE
I can use a simple Morphological
Image Cleaning Algorithm to find the
hidden message.
CHARLIE (cont'd)
The algorithm was originally intended
to save corrupted images, but it's
also useful to smooth out the grayscale
image, removing the camouflage
while revealing the thin features
where a hidden message resides.
DON
How long will it take?
CHARLIE
Get a cup of coffee.
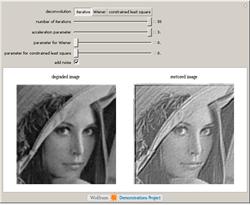
This Demonstration applies various
deconvolution techniques to restore original images from blurred images. Mathematically, a linearly
degraded (blurred) image is defined as the
convolution of the pristine image with a kernel function with additive
noise. The problem is to find a best estimate of the
pristine image from the noisy blurred data when the noise function is unknown.




