NUMB3RS Episode 411: Breaking Point--Wolfram Research Math Notes

EXT. FBI - IN FRONT OF LOBBY - DAY

The unreasonable effectiveness of mathematics

[ XXXXXXX REMOVED FROM PRODUCTION SCRIPT XXXXXXX ]

                    CHARLIE
          It's simple.  Math "fits" our world
          to an uncanny degree.  It gives us
          a power of... prediction.

                    REPORTER
          In an academic sense, I suppose,
          maybe...

                    CHARLIE
          No, not in an academic sense...
             (then, genuine)
          You're seeing math as just some
          book full of tables and theorems...
          That's like looking at the universe
          and seeing nothing but gasses and
          dust.  Math isn't a mechanism for
          finding answers; math is the
          answers.  And it's our mission...
          our obligation, to ask the right
          questions.

[ XXXXXXX REMOVED FROM PRODUCTION SCRIPT XXXXXXX ]

Physicists and mathematicians alike have long considered and attempted to explain just how it is that mathematics can be so effective in describing so many different aspects of physical reality and the structure of the world and universe when it is based on such a relatively small set of simple rules. In a famous 1960 paper entitled "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," physicist Eugene Wigner pondered the enormous and uncanny usefulness of mathematics in the natural sciences, characterizing it as something bordering on the mysterious, given that there is no rational explanation for it. Wigner emphasized that the mathematical structure of a physical theory leads to theoretical advances and empirical predictions so frequently that it must reflect some larger and deeper truth about both mathematics and physics. Wigner's thoughts and conclusions were subsequently considered by applied mathematician Richard Hamming in his 1980 paper, "The Unreasonable Effectiveness of Mathematics."

If the reporter in this scene is not swayed by the arguments of Wigner and Hamming, his skepticism might perhaps be changed upon learning about a 2006 homicide case in Richmond, Virginia. Professor Michael Black of Brown University was contacted for assistance in identifying the suspect's car from distorted, blurry surveillance footage. Using Markov random fields, statistical modeling, de-ghosting, and a host of computer vision techniques, Professor Black and a group of students calibrated the car's wheelbase, which led them to posit the car's make as a 1992-1994 Camry with a sunroof, eliminating all but 600 of the possible 76,000 registered Camrys. Using measurements from fixed objects at the murder site, they also theorized the suspect's height to be 5'6"-5'7". Police investigators from Henrico County praised the tenacity of the scientists and valued their findings: "We've got something where we had nothing. Eventually, this guy is going to get caught."

INT. FBI - WAR ROOM - DAY

Asymmetric threat assessment

                    CHARLIE
          It's called an Asymmetric Threat
          Assessment.  We've done threat
          assessments before... but I think I
          can use this one to analyze and
          calculate motive...

                    COLBY
          But Charlie, all 28 suspects are
          presumably after the same thing,
          revenge.

                    CHARLIE
          True.  But each one has been
          motivated to a different degree...
              (then)
          Look.  Think of that cool carnival
          game where you shoot a squirt gun
          in the clown's mouth in order to
          fill your balloon...

AUDIENCE VISION - The carnival game.  All eight seats are
filled as the Carnival WORKER moves down the line, collecting
dollar bills...

                    CHARLIE (cont'd)
          An asymmetric threat assessment
          allows us to measure the factors
          that feed motive in each suspect...

The Carnival Worker hits the start button.  A bell SOUNDS and
the squirt guns begin firing water...

                    CHARLIE (cont'd)
          ... in the same way the mechanism
          of the game measures the flow of
          water into each clown's mouth.

As the balloons fill...

                    CHARLIE (cont'd)
          It doesn't matter whether the
          suspects have the same motive or
          not.  We only need to identify the
          one case in which the motive has
          been fed to the point where the
          suspect eventually pops.

BOOM!  One of the balloons explodes.

END VISION --

The term "asymmetric threat" refers to the use of crude, low-tech methods to attack a superior high-tech enemy. Needless to say, this topic has received increased attention following the September 11 attacks in the United States. Various mathematical models have been applied to asymmetric threat assessment, including hidden Markov models, Bayesian networks, and game theory.

A hidden Markov model is a statistical model in which the system being modeled is assumed to be a Markov process, that is, a random process whose future probabilities are determined by its most recent values having unknown parameters, and unknown ("hidden") parameters are assumed to exist in the model that can be derived from the observable parameters. It is possible to infer the entire set of parameters; these can then be used to perform a more complete analysis of the underlying phenomenon being modeled.

A Bayesian network (a term coined by Judea Pearl) is a graphical model (formally, an acyclic digraph whose vertices represent variables and whose edges encode conditional independencies between the variables) that represents a set of variables together with the probabilities of their being independent.

Game theory has been discussed in a number of previous episodes, including Episode 409, "Graphic."

INT. EPPES HOUSE - GARAGE - NIGHT

Large numbers

                    AMITA (cont'd)
          Threat assessment?

                    CHARLIE
          Yeah, for Don's missing reporter.
              (re: the laptop)
          It's running, but I keep refining
          the algorithm.

                    AMITA
          Wow.  That's a pretty large value
          for "n."

                    CHARLIE
          She had a lot of enemies.

The symbol most commonly used to represent the size of an integer-valued quantity in mathematics is the letter n (also commonly written in upper case, that is, N). For example, the sample size in a statistical test is commonly denoted in this way, so the mean of a set of quantities x₁, x₂, ..., is given by

$x-bar = 1/n sum_{i=1}^n x_i$

It would be quite natural for a mathematician to refer to something that has a large integer value as "having a large n."

A wide variety of large numbers crop up in mathematics. Some are contrived, but some actually arise in proofs. Often, it is possible to prove existence theorems by deriving some potentially huge upper limit that is frequently greatly reduced in subsequent versions; for example, Graham's number (related to the combinatorial problem of finding the smallest way to guarantee the existence of four committees in which all pairs fall in the same group and all the people belong to an even number of committees), Kolmogorov-Arnold-Moser theorem (a deep result in chaos theory that originally required functions to be smooth up to their 333rd derivatives but has since been reduced to slightly more than their 2nd), Mertens conjecture (a conjecture concerning the summatory function of the Möbius function, known as the Mertens function, which has at least one counterexample for ), Skewes number (given below, which is related to an inequality involving the prime counting function and logarithmic integral), and Wang's conjecture (a refuted conjecture related to periodic tiling in which the initial counterexample required 20426 tiles but the best currently known is 13).

$Sk = e^e^e^79 \approx 10^10^10^34$

Readers may recall Charlie's reference to the strong law of small numbers ("There aren't enough small numbers to meet the many demands made of them") in Episode 404, "Thirteen."

Not surprisingly, there is also a law of large numbers, which is one of several theorems expressing the idea that as the number of trials of a random process increases, the percentage difference between the expected and actual values goes to zero. A somewhat tongue-in-cheek result, going by the name of the "frivolous law of arithmetic," states that almost all natural numbers are very, very, very large.

Another result known as the law of truly large numbers, due to Persi Diaconis and Frank Mosteller, states that with a large enough sample, any outrageous thing is likely to happen. Mathematician John E. Littlewood considered an event that occurs one in a million times to be "surprising." Taking this definition, close to 100000 surprising events are "expected" each year in the United States alone and, in the world at large, one can be absolutely sure to see incredibly remarkable events! This is closely related to coincidences, which are surprising concurrences of events perceived as meaningfully related, with no apparent causal connection. Given a large number of events, extremely unlikely coincidences are possible--and perhaps even common. To quote Sherlock Holmes from "The Adventure of the Blue Carbuncle":

"Amid the action and reaction of so dense a swarm of humanity, every possible combination of events may be expected to take place, and many a little problem will be presented which may be striking and bizarre..."

INT. CALSCI - HALLWAY/CHARLIE'S OFFICE - DAY

Subtended angles

Charlie walks through the hall, repeatedly glancing back at
David, who walks several steps behind him. Finally --

                    CHARLIE
          This is crazy having a bodyguard.
          Do you really have to lurk like
          that?

                    DAVID
          Yes.  I've got a better vantage
          point back here.  I can see more.

                    CHARLIE
          More what?  C'mon, David --

David's statement can be taken as a simple consequence of the mathematical fact that the angle subtended by a given object from a point decreases as its distance increases. In other words, more of David's view is blocked by Charlie when he's closer than when he's far away.

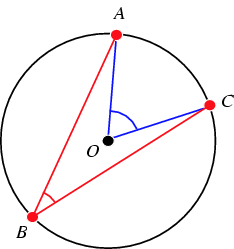
There is also some beautiful mathematics in the subtending of angles in a circle. A theorem known to Euclid (and given in proposition III.20 in his Elements) states that for an inscribed angle ABC and a central angle AOC with the same endpoints on a circle, AOC = 2 ABC. This proposition also turns out to have a fascinating historical connection with Albert Einstein.

INT. EPPES HOUSE - GARAGE - DAY

Mathematics of real estate

Charlie and Colby charge up to David at his desk --

                    CHARLIE
          Real estate.  The numbers describe
          individual properties - 10 digit
          property ID numbers, square
          footage, tract numbers, assessed
          values.  Only it was all obscured.

                    COLBY
          Bonnie Parks must have had a source
          inside the County Assessor's Office
          who was feeding her info.

                    DAVID
          But that's all public record stuff.
          Why bother to disguise it with a
          code?

Not surprisingly, a great deal of mathematics has been brought to bear on the modeling of real estate prices. Such models include techniques such as spatial autoregression, normalized distance-weighted sums of stationary processes, spatial-temporal forecasting, and hedonistic regression (essentially, regressions of rent or house values against characteristics of the unit that determine rent or value). See the references for many papers on the subject.

References

Alexseev, M. A. Without Warning: Threat Assessment, Intelligence, and Global Struggle. Palgrave Macmillan, 1997.

Clapp, J. M. "Semiparametric Method for Estimating Local House Price Indices." Real Estate Econ. 32, 127-160, 2004.

Conan Doyle, A. "The Adventure of the Blue Carbuncle." The Strand, Jan. 1892. Reprinted in The Complete Sherlock Holmes. New York: Doubleday, pp. 244-257, 1988.

Diaconis, P. and Mosteller, F. "Methods of Studying Coincidences." J. Amer. Statist. Assoc. 84, 853-861, 1989.

Dubin, R.; Pace, R. K.; and Thibodeau, T. G. "Spatial Autoregression Techniques for Real Estate Data." J. Real Estate Lit. 7, 79-95, 1999.

Hamming, R. "The Unreasonable Effectiveness of Mathematics." Amer. Math. Monthly 87, 1980. http://www.ccrnp.ncifcrf.gov/~toms/Hamming.unreasonable.html

Heeringa, B. and Cohen, P. "An Underlying Model for Defeat Mechanisms." In Proceedings of the 2000 Winter Simulation Conference (Ed. J. A. Jones, R. R. Barton, K. Kang, and P. A. Fishwick). pp. 933--939, 2000.

Institute for Mathematics and Its Applications. "Real-Life NUMB3RS." http://www.ima.umn.edu/nuggets/murder.html

Littlewood, J. E. Littlewood's Miscellany. Cambridge, England: Cambridge University Press, 1986.

Pawlowski, A. M.; Gigli, S.; and Vetesi, F. J. "Situation and Threat Refinement Approach for Combating the Asymmetric Threat." Lockheed Martin Advanced Technology Laboratories. Camden, NJ.

Pearl, J. Causality: Models, Reasoning, and Inference. Cambridge, England: Cambridge University Press, 2000.

Singh, S.; Donat, W.; Tu, H.; Lu, J.; Pattipati, K.; and Willett, P. "An Advanced System for Modeling Asymmetric Threats." In 2006 IEEE International Conference on Systems, Man, and Cybernetics. October 8-11, 2006, Taipei, Taiwan. PDF

Wigner, E. "The Unreasonable Effectiveness of Mathematics in the Natural Sciences." Comm. Pure Appl. Math. 13, 1-14, Feb. 1960. http://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html