Interactive Computations

Use the free Wolfram Mathematica Player to interact with the math behind NUMB3RS.

                   COLBY
          Gives us eleven points, including the
          meth lab.  I see a map with a bunch of
          dots on it -- I figure you can tell
          me something -- maybe even find his
          stash house --

Basic Statistics of Movable Points

See how various location measures (such as arithmetic mean, median, root-mean-square, geometric mean, and harmonic mean) change as you move points around.

                   CHARLIE
          We know the order that the locations
          were arrived at -- what about doing a
          time series analysis of overlapping
          Dirichlet Tessellations?

Larry considers this for a beat -- then --

                   LARRY
          Wow.

Voronoi Diagrams

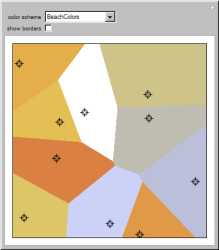
The Voronoi diagram (also called Dirichlet tessellation) for a set of points S in the plane is a partition of the plane into convex polygons, each of which consists of all the points in the plane closer to one particular point of S than to any other.

Colby sits at a computer, running through a SERIES OF MUG
SHOTS as Don enters...

                   DON
          Any luck?

                   COLBY
          Facial recognition software, my brain
          is not.  But I've been through Intel's
          whole dossier on The New American
          Front, and I'm pretty sure he isn't in
          there.  Hooper giving us anything yet?

Emotion Tiling

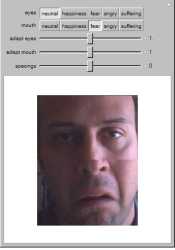
Facial expressions of happiness, fear, anger, and suffering can be reduced to the shapes of eyes and mouths. As suggested by Adolphs, Tranel and Damasio, and Patrik Vuilleumier, the perceived emotions in facial expressions involve processing by the amygdala.

Charlie, Amita, and Larry a swirl of activity, as, on
THE MAP --

Almost an inversion of what we've previously seen; the
spiderwebbed cracks are faded, and the highlighted zones
are where no streets had been touched --

                   CHARLIE
          How're we doing with the cluster
          radius changes?

                   AMITA
          Almost entered --

Cluster Analysis for 2D Points

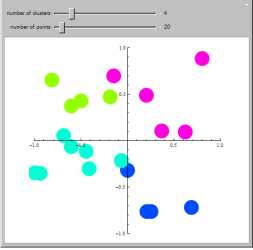
Cluster analysis groups data elements according to a similarity function. In this case, the similarity function is simply the Euclidean distance function, which allows us to group them into clusters automatically based on how close they are.