CHARLIE packs a duffel with sweatpants, T-shirts and a towel.
AMITA watches as he shoves the contents into the bag.
AMITA
You're making a mess.
(grabs it)
Let me do it.
She folds the T-shirt with perfection.
CHARLIE
An exact hundred and eighty degree
fold, what I'd expect from a master
of combinatorics.
AMITA
Actually, I worked at the Gap in
high school.
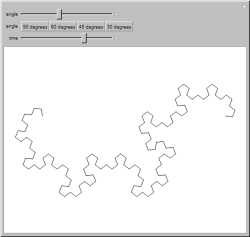
Fold a piece of paper in half repeatedly and
then unfold the folds uniformly using the same
angle. For each angle choice, you get a different
fractal curve; these are called
dragon curves. The folding is a predictable
substitution system, which causes successive
elements to alternate which way they kink out.
CHARLIE
Imagine an uncut diamond...
MEGAN
Not a problem --
ENTER AUDIENCE VISION
Of a large, uncut diamond.
CHARLIE (V.O.)
The diamond is beautiful, but to
make it more valuable, you have to
cut the diamond perfectly.
Zoom into the diamond.
CHARLIE (V.O.) (cont'd)
Under a microscope, the facets of
the diamond are intertwined.
We see the fine lines of the diamond connected.
CHARLIE (V.O.) (cont'd)
In order to get the maximum profit
out of the diamond you must cut or
untwine the facets.
The diamond is cut, falls into four smaller and more
brilliant pieces.
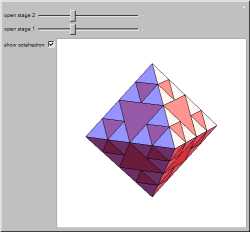
Six
octahedra are placed at the vertices of a
larger octahedron. The voids within the large octahedron are filled with
tetrahedra to form a composite solid
octahedron, which is then placed at the vertices of yet another octahedron, and the voids again are filled with
tetrahedra. This process constitutes two stages of a
fractal structure.
Don studies the photo.
DON
Charlie's helped us find locations
based on the shadow of the sun
before...
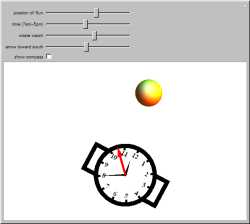
You can use an analog wristwatch to locate the direction of south during daylight hours. It is assumed that you live in
the Northern Hemisphere, not too close to the equator or the North Pole. Hold your watch horizontally and turn it so
that the hour hand points in the direction of the sun. South is then halfway between this direction and twelve o'clock,
which you can mark with the red arrow in this Demonstration.
David plays chess on his computer. Colby next to him. Megan
approaches in the background.
DAVID
Alright, Knight to c3...
ON SCREEN - his knight moves. Then, it's the computer's turn.
David gets checkmated. YOU LOSE pops up in big letters.
DAVID (cont'd)
Damn it --
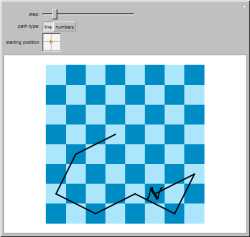
This shows a
knight's tour starting from any
position on a
chessboard. A classic
chess problem is to find a sequence of moves such
that a knight will land on every square exactly once. First position the knight anywhere on the board.
LARRY
You know Charles, I'm all for new
adventures but the suspense is
really starting to get to me.
MEGAN
This from a man who lived a hundred
miles above the earth...
LARRY
Two hundred twenty-four to be
exact.
October 2007 marks the 50th anniversary of the launch of the Russian satellite Sputnik 1, the first human-made object to
orbit the Earth. The satellite was carried into orbit on a Soviet R-7 rocket and had a height of 228 km at perigee
(closest point to Earth) and a height of 945 km at apogee (farthest point from Earth). Its velocity at perigee was 8
km/s and its time for completing one orbit was 96 minutes. Sputnik 1 stayed in orbit for three months before falling to
Earth in January 1958.





