

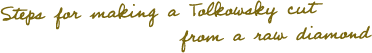
The mathematics of folding
CHARLIE packs a duffel with sweatpants, T-shirts and a towel.
AMITA watches as he shoves the contents into the bag.
AMITA
You're making a mess.
(grabs it)
Let me do it.
She folds the T-shirt with perfection.
CHARLIE
An exact hundred and eighty degree
fold, what I'd expect from a master
of combinatorics.
AMITA
Actually, I worked at the Gap in
high school.
There are many mathematical and recreational problems related to folding. Origami, the Japanese art of paper folding, is one well-known example. The Season 2 episode "Judgment Call" featured Charlie discussing the types of folds in origami.
It is possible to make a surprising variety of shapes by folding a piece of paper multiple times, making one complete straight cut, then unfolding. For example, as illustrated by Erik D. and Martin L. Demaine, a pentagram can be obtained after four folds, as can a polygonal swan, butterfly, and angelfish. Amazingly, every polygonal shape can be produced this way, as can any disconnected combination of polygonal shapes. Furthermore, algorithms for determining the patterns of folds for a given shape have been devised by Marshall Bern, Erik D. Demaine, David Eppstein, and Barry Hayes.
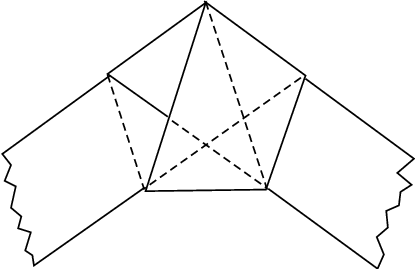
The figure above illustrates the construction of a regular pentagon using paper folding.
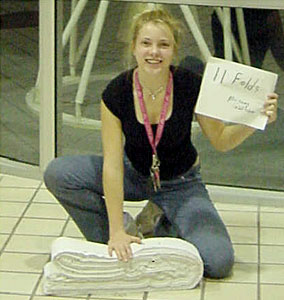
As a high school student, Britney Gallivan set a new world record by folding in half first gold foil, then paper, a whopping 12 times in January of 2002, thus debunking the widespread assertion that paper cannot be folded in half more than eight times. Britney and her feat were mentioned in the Season 1 episode "Identity Crisis."
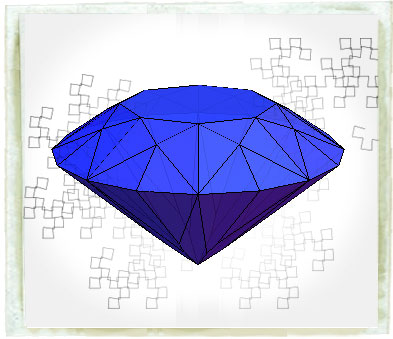
Diamond cutting
CHARLIE
Imagine an uncut diamond...
MEGAN
That's not a problem --
ENTER AUDIENCE VISION
Of a large, uncut diamond.
CHARLIE (V.O.)
When the diamond's discovered, it's
a large uncut stone.
Zoom into the diamond.
CHARLIE (V.O.) (cont'd)
Under a microscope, the flaws and
inclusions become visible.
We see the fine lines of the diamond connected.
CHARLIE (V.O.) (cont'd)
To maximize profit, they have to cut
the stone to remove the imperfections
so that the valuable and brilliant
facets are revealed.
The diamond is cut, falls into four smaller and more
brilliant pieces.
While diamond cutting dates back to the Middle Ages, the sophistication and types of cuts have evolved over time, culminating in the so-called brilliant cuts. The brilliance and sparkle of a diamond comes from its high index of refraction in combination with the specially chosen angles between the faces (known as dihedral angles). The different radii and heights of diamond faces are precisely prescribed, with Marcel Tolkowsky's classical shape of 57 faces with parameters chosen to make the appearance of the cut diamond especially pleasing.
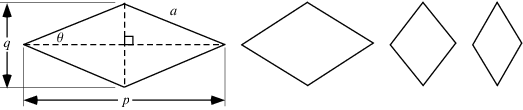
The term "diamond" is used in mathematics to variously refer to a rhombus (illustrated above) or the special case of a square tilted at a 45° angle.
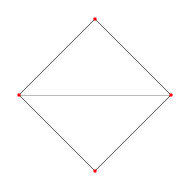
The diamond graph is the simple graph on four nodes and five edges as illustrated above.
Supervised multiclass labeling
Don hands Charlie the partial photo of the mountain range.
DON (cont'd)
Think you can dial us into the
location?
CHARLIE
(rubs his head)
Supervised Multiclass Labeling.
(then)
Imagine a cadaver dog searching for
a body...
ENTER AUDIENCE VISION
Bloodhound tracks through the woods.
CHARLIE (V.O.) (cont'd)
If you show the dog a photo of the
subject, it's useless.
Dog stares at the photo of the missing person (man), tries to
eat the picture.
CHARLIE (V.O.) (cont'd)
Give him a piece of clothing,
though, and the dog keys off the
scent.
Hound sniffs a shirt and takes off like a bat out of hell...
CHARLIE (V.O.) (cont'd)
The SML algorithm looks for its own
information or scent...
Our photo appears, above it are a series of numbers... Dog
next to it.
CHARLIE (cont'd)
-- by scanning millions of images
on the internet to look for a
match...
Above that a second row of numbers cycle through.... when it
finds a match, the dog starts barking.
We all are familiar with searching text documents for words, phrases, and sentences. The automated search and selection of images based on textual descriptions of their content is much less developed. Understanding the content of an image is a difficult and computationally intensive process. Last year, researchers Gustavo Carneiro, Antoni B. Chan, Pedro J. Moreno, and Nuno Vasconcelos from the University of California, San Diego announced a potentially revolutionary new algorithm called supervised multiclass labeling (SML). This algorithm is shown many images and learns to identify certain characteristics of certain objects as well as to identify features that differentiate two objects. As the word supervised suggests, the algorithm is not just a black box, but requires (initially) a large number of well-defined inputs from humans to teach the program the objects to recognize and to differentiate. Looking for images with mountains was one of the test cases shown in the original press release announcing the new method. The algorithm is probabilistic in nature and uses local as well as global features of the images. By segmenting an image into small parts, characteristics of objects can be extracted and learned.
A central mathematical cornerstone of the algorithm is Bayesian analysis, especially the estimation of the posterior probability from the prior probability and the probability of the occurrence of a certain feature within a certain class, which is a variant of the Bayes theorem.
The method has been extended to songs and allows the classification and retrieval of relevant songs. A Google Tech Talk about the algorithm was presented by Nuno Vasconcelos on September 25, 2006.
Chess
David plays chess on his computer. Colby next to him. Megan
approaches in the background.
DAVID
Alright, Knight to c3...
ON SCREEN - his knight moves. Then, it's the computer's turn.
David gets checkmated. YOU LOSE pops up in big letters.
DAVID (cont'd)
Damn it --
Chess is a two-player board game believed to have been played in India as early as the sixth century AD. Different chess games are played in different parts of the world. The variants played most often are western chess, Shogi (in Japan), and Xiangqi (in China).
The western version of chess is a game played on an eight by eight board, called a chessboard, of alternating black and white squares. Pieces with different types of moves are placed on the board: a set of black pieces in the first two rows and a set of white pieces in the last two rows. The pieces are called the bishop (2), king (1), knight (2), pawn (8), queen (1), and rook (2). The object of the game is to capture the opponent's king.
The analysis of chess is extremely complicated due to the many possible options at each turn. However, there are entire books consider that clever end-game positions, which may be analyzed completely.
English mathematician Godfrey Harold Hardy (1877-1947), perhaps most famous for his discovery of and work with Indian mathematical genius Srinivasa Ramanujan (Amita's namesake), estimated the total number of possible games of chess as 10^(10^(50)). The number of possible games of 40 moves or less, P(40), is approximately 10^(40), a number arrived at by: (1) estimating the number of pawn positions (in the no-captures situation, this is 15^8); (2) multiplying by the possible positions for all pieces; and (3) dividing by two for each of the (rook, knight) pairs that are interchangeable, and dividing by two for each pair of bishops (since half the positions will have the bishops on the same color squares). Mathematician and father of information theory Claude Shannon gave the estimate
Let the term "chess diagram" refer to possible chess arrangements not including castling and en passant moves. Then the numbers of possible chess diagrams after n plies for n = 0, 1, ... are given by 1, 20, 400, 5362, 71852, 815677, 9260610, 94305342, 958605819, ... (sequence A019319 in Neil Sloane's On-Line Encyclopedia of Integer Sequences).
There are many interesting mathematical problems inspired by chess, including the bishops problem, kings problem, knights problem, knight's tour, queens problem, and rooks problem.
Short chess games
David studies the board, makes a move then pulls it back.
Bishop rolls his eyes. David concentrates, taking his time --
peeks at his notes...
BISHOP
C'mon man, I got a life to lead.
David moves. Satisfied, looks at Bishop.
DAVID
Your move --
He barely gets the words out -- Bishop's hand moves in a
blur. Then, David... Then, Bishop... Then --
BISHOP
Checkmate.
Bishop takes his ten dollars. David, humiliated, removes
another ten from his pocket.
BISHOP (cont'd)
It's your money.
DAVID
Let's go.
Bishop re-sets the pieces.
David moves...
Bishop moves...
David moves...
Bishop moves... and,
BISHOP
Checkmate. Had enough?
In this scene, there are a number of short checkmates. For time considerations, the games were kept to six plies (or three turns), which essentially demands a variation of the so-called fool's mate. The numbers of different possible chess games that result in a checkmate in n moves for n = 1, 2, ... are given by 0, 0, 0, 8, 347, 10828, 435767, 9852036, ... (sequence A079485 in the On-Line Encyclopedia of Integer Sequences). In other words, after four plies (on black's second turn), there are eight possible checkmates, and on the fifth ply, there are 347 possible games where white's third turn checkmates black.
n-dimensional data sets
Charlie looks at the screens.
CHARLIE
Dimensional Data Sets....
AMITA
Each week... this guy J-Light
teaches his protege, Bishop, a
chess lesson...
LARRY
(points)
David thinks a code is being passed
within the lesson.
Humans are used to seeing objects in two- or three-dimensional space. However, much real-world data exists naturally in a much higher dimension. As a simple example, imagine a car driving on a curved road. Its position can be represented by two coordinates: x and y. However, the velocity of the car as specified by the two variables vx and vy (the velocity components in the x and y directions, respectively) provides two additional dimensions. The car therefore requires a four-tuple of coordinates (x, y, vx, vy) to specify its state at any given point it time. (In physics, because of the importance of the space of positions and velocities, this space is known as "phase space.") Frequently data from measurements has even more dimensions (such as acceleration, stresses, angular momenta, etc.). There exist various algorithms to analyze data that lives in a high-dimensional space, including cluster analysis (see Episode 413, "Black Swan") and projecting the data into a lower-dimensional space which allows easier visualization.
Even such simple objects as the sine function y(x) = sin(x), typically displayed in two dimensions as an oscillating curve, exists much more naturally in four dimensions when both x and y and considered as complex variables through the four-tuple (Re(x), Im(x), Re(sin(x)), Im(sin(x))), where Re denotes the real part and Im the imaginary part. Looking at the resulting surface from different directions shows the true wealth and beauty of the sine function, a form of visualization know as a tetraview.
References
Bern, M.; Demaine, E.; Eppstein, D.; and Hayes, B. "A Disk-Packing Algorithm for an Origami Magic Trick." Proc. Internat. Conference of Fun with Algorithms, Isola d'Elba, Italy. pp. 32-42, 1998.
Carneiro, G.; Chan, A. B.; Moreno, P. J.; and Vasconcelos, N. "Supervised Learning of Semantic Classes for Image Annotation and Retrieval." IEEE Trans. Patt. Anal. Mach. Intell. 29, 394-410, 2007. [PDF]
Demaine, E. D. and Demaine, M. L. "Fold-and-Cut Magic." In Tribute to a Mathemagician (Ed. B. Cipra, E. D. Demaine, M. L. Demaine, and T. Rodgers). Wellesley, MA: A K Peters, pp. 23-30, 2004.
Demaine, E. D.; Demaine, M. L.; and Lubiw, A. "Folding and Cutting Paper." In Revised Papers from the Japan Conference on Discrete and Computation Geometry (Ed. J. Akiyama, M. Kano, and M. Urabe). Tokyo, Japan: Springer-Verlag, pp. 104-117, 1998.
Demaine, E. K.; Demaine, M. L.; and Lubiw, A. "Folding and Straight Cut Suffice." In Proc. 10th Annual ACM-SIAM Symposium Disc. Alg. Baltimore, MD: ACM Press, pp. 891-892, 1999.
Gallivan, B. C. "How to Fold Paper in Half Twelve Times: An 'Impossible Challenge' Solved and Explained." Pomona, CA: Historical Society of Pomona Valley, 2002.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. Providence, RI: Amer. Math. Soc., p. 17, 1999.
Paulsen, J. (Ed.) "Diamond Design: A Study of the Reflection and Refraction of Light in a Diamond by Marcel Tolkowsky."
Shannon, C. "Programming a Computer for Playing Chess." Phil. Mag. 41, 256-275, 1950.
Tolkowsky, M. Diamond Design: A Study of the Reflection and Refraction of Light in a Diamond. London: E. & F.N. Spon, Ltd., 1919.
Turnbull, D.; Barrington, L.; Torres, D.; and Lanckriet, G. "Semantic Annotation and Retrieval of Music and Sound Effects." IEEE Trans. Audio, Speech, Language 16, 467-476, 2008.
Vasconcelos, N. "Using Statistics to Search and Annotate Pictures." Google Tech Talk. September 25, 2006. http://video.google.ca/videoplay?docid=2225647906131550844.
Wikipedia. Diamond Cut.