

Combinatorial matrix theory (again)
AMITA packs her bag for class as CHARLIE writes a list on the
board-- Non-negative matrices, linear programming, symmetric
matrices, etc.
CHARLIE
Shall we call it 'Matrix Theory
with Combinatorics?'
AMITA
How about 'Combinatorial
Applications?' We should teach
together-- you explain the theory,
I show the applications.
CHARLIE
Great, when are you free to plan
presentations?
AMITA
(ready to leave)
I'm teaching until four, then I
have office hours until six. After
that, over dinner?
CHARLIE
Sure.
As we know from Episode 407, "Primacy," Amita's teaching and research interests include combinatorial matrix theory. This is a rich branch of mathematics that combines combinatorics, graph theory, and linear algebra.
Nonnegative matrices
Nonnegative matrices are important in a variety of applications and have a number of attractive mathematical properties. Together with positive semidefinite matrices, they serve as as a natural generalization of nonnegative real numbers. The most fundamental properties of nonnegative matrices require fairly advanced mathematics and were established by Oskar Perron in 1907 and Ferdinand Georg Frobenius 1912. To quote Charles Johnson in his review of the classic text on the subject by Abraham Berman and Robert J. Plemmons, "Important properties [of nonnegative matrices] are still being discovered, and, typical of much of modern research in matrix theory, the work often involves an attractive marriage of algebra, analysis, combinatorics, and geometry."
Linear programming
Linear programming refers to optimizing an outcome using a linear mathematical model together with a set of constraints. In the Season 4 opening episode "Trust Metric," Charlie used set covering deployment (a particular application of a specialized type of linear programming) to help place police units optimally. In the same episode, he also remarked, "You don't need Karmarkar's algorithm" to mean "You don't need to be a rocket scientist to know...." In that quote, Karmarkar's algorithm refers to a so-called interior point method of linear programming that is generally much more efficient than traditional techniques (such as the simplex method).
Symmetric (and antisymmetric) matrices
A symmetric matrix is a square (and generally real) matrix whose transpose (i.e., the matrix obtained by interchanging rows and columns) equals itself. An antisymmetric matrix is similarly defined as a matrix whose transpose is the negative of itself. Symmetric matrices are especially important in mathematics and physics because the generalization of symmetric matrices to the case of matrices having complex-valued elements are objects known as Hermitian matrices, which are fundamental in the theory of quantum mechanics and its relativistic generalizations.
Matrices may be decomposed into their symmetric and antisymmetric parts via
where
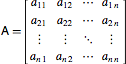 and
and
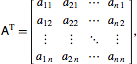
so
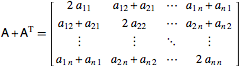
(twice the symmetric part), which is symmetric, and
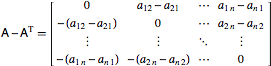
(twice the antisymmetric part), which is antisymmetric, and half the sum of these gives the original matrix.
Fish bladders, lenses, and intersecting circles
LARRY
(re: the board)
Do you know what this is?
CHARLIE
A Venn Diagram Intersection
indicating suspects who match the
description and have a history of
violence. I'm helping Don.
LARRY
It's also an ancient religious
symbol-- you may recognize it--
(outlines the "fish")
The Vesica Piscis, symbolizing the
meeting of heaven and earth.
Megan has entered, seeing what Larry's drawn.
MEGAN
You know the coolest things--
Lenses
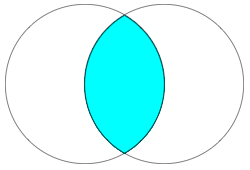
In mathematics, a lens is a convex plane figure composed of two circular arcs. The term vesica piscis (Latin for fish bladder) is often used to refer to the particular lens formed by the intersection of two unit circles whose centers are offset by a unit distance--a configuration illustrated above. Here, the lens is indicated as the two dark black curves enclosing the shaded interior region. The symmetric lens obtained in this way has been endowed with various mystical properties through the ages, apparently first among the Pythagoreans, who considered it a holy figure. Renaissance artists also frequently surrounded images of Jesus with the vesica piscis.
The height-to-width-ratio of the vesica piscis is equal to ![]() , the square root of 3, a number sometimes known as Theodorus's constant. Compare this to
, the square root of 3, a number sometimes known as Theodorus's constant. Compare this to ![]() , the square
root of 2, which is sometimes known as Pythagoras's constant and was of even more significance to the Pythagoreans. In fact, legend holds
that the Pythagorean philosopher Hippasus used geometric methods to demonstrate the irrationality of
, the square
root of 2, which is sometimes known as Pythagoras's constant and was of even more significance to the Pythagoreans. In fact, legend holds
that the Pythagorean philosopher Hippasus used geometric methods to demonstrate the irrationality of ![]() (i.e., the
fact that this number cannot be expressed as the ratio of any two integers) while at sea and, upon notifying
his comrades of his great discovery, was immediately thrown overboard by the fanatic Pythagoreans.
(i.e., the
fact that this number cannot be expressed as the ratio of any two integers) while at sea and, upon notifying
his comrades of his great discovery, was immediately thrown overboard by the fanatic Pythagoreans.
Note that we encountered circle intersections previously in Episode 401, "Trust Metric", as well as in Episode 409, "Graphic." The area of a lens, corresponding to the area of overlap indicated in aqua above, can be determined directly from the trigonometric formula given in the Episode 409 notes and reproduced above by setting d = r = R = 1. Alternately, it can derived with the help of a little integral calculus, which is especially easy using Mathematica's ability to integrate over regions specified by inequalities (this is done internally using cylindrical algebraic decomposition) as follows:
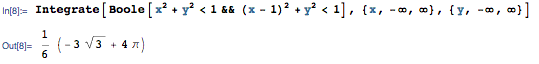
In the above piece of code, the two inequalities are simply those specifying the interiors of the two circles whose intersection gives the lens. This produces the beautiful result:
Lunes
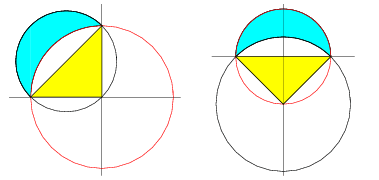
Geometric figures related to lenses that consist of crescent-shaped (i.e., concave) regions bounded by two circular arcs of unequal radii were also considered by the ancient Greeks and are known as lunes. In each of the figures above, the area of the lune (filled in blue) is equal to the area of the indicated triangle (filled in yellow). Hippocrates of Chios squared the above left lune as well as two others in the 5th century BC. Two more squarable lunes were found by T. Clausen in the 19th century. Not until the 20th century did N. G. Tschebatorew and A. W. Dorodnow finally prove that these are the only five squarable lunes.
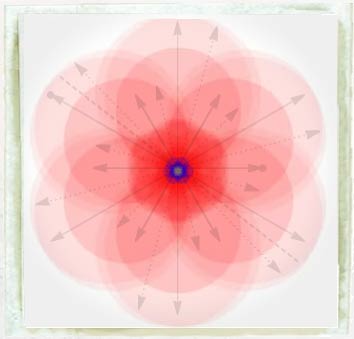
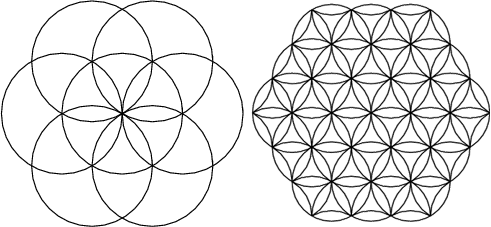
Mystical circle arrangements
There are many attractive arrangements of circles that give symmetrically placed lens-shaped regions, including a number found at the Temple of Osiris at Abydos, Egypt. Configurations sometimes known as the seed of life (which also appeared in Italian art from the 13th century) and the flower of life (which appeared in Phoenician art from the 9th century BC) are illustrated below.
Venn diagrams
CHARLIE
Venn diagrams are illustrations
used in set theory, showing
relationships among groups of
things. We've deepened the
analysis from what you learned in
school by adding dimensions.
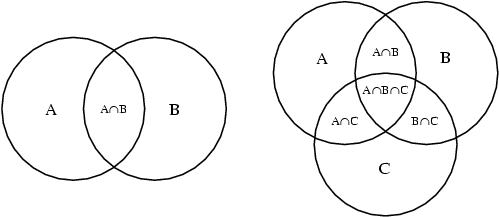
A Venn diagram is a schematic diagram used in logic theory to depict collections of sets and represent their relationships. The Venn diagrams on two and three sets are illustrated above. The order-two diagram (left) consists of two intersecting circles, producing a total of four regions, A, B, A ∩ B, and the empty set ∅, represented by none of the regions occupied. Here, A ∩ B denotes the intersection of sets A and B. The order-three diagram (right) consists of three symmetrically placed mutually intersecting circles comprising a total of eight regions. The regions labeled A, B, and C consist of members that are only in one set and no others; the three regions labeled A ∩ B, A ∩ C, and B ∩ C consist of members that are in two sets but not the third; the region A ∩ B ∩ C consists of members that are simultaneously in all three; and no regions occupied represents ∅.
In general, an order-n Venn diagram is a collection of n simple closed curves in the plane with the following properties:
 |
The left figure above is an n = 5 Venn diagram by Branko Grünbaum, while the attractive 7-fold rosette illustrated in the middle figure is an n = 7 Venn diagram, called "Victoria" by Frank Ruskey. The right figure shows a recently constructed symmetric Venn diagram on n = 11, due to Ruskey, Carla Savage, and Stan Wagon. See the papers and online material in the references section below for many more details and attractive figures, as well as for interesting recent developments in the field of Venn diagram research.
The Higgs boson
LARRY
Dr. Ramanujan, I have a proposition
for you.
AMITA
(teasing)
Better not tell Charlie...
LARRY
Once or twice in a lifetime there
are quests that require all we have
to give and more. I am embarking
on such a quixotic adventure and in
thinking on who should be my Sancho
Panza I come up with only one name--
yours.
AMITA
Larry, what are you talking about?
LARRY
I've accepted the D Zero team's
offer to search for the Higgs Boson
and I require a computational
partner.

As already discussed in Episode 407, "Primacy," one of the main unconfirmed aspects of the "standard model" that unites three of the four known forces of the universe is the existence (and the properties) of the so-called Higgs boson. This particle is a very important theoretical ingredient of the theory, so finding it in Nature is important to ensure the full correctness of the standard model. A schematic animation of Higgs emission is shown at right.
References
Berman, A. and Plemmons, R. J. Nonnegative Matrices in the Mathematical Sciences. SIAM, 1994.
Dunham, W. "Hippocrates' Quadrature of the Lune." Ch. 1 in Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 1-20, 1990.
Frobenius, G. "Über Matrizen aus nicht negativen Elementen." S.-B. Preuss. Akad. Wiss. (Berlin), pp. 456--477, 1912.
Grünbaum, B. "On Venn Diagrams and the Counting of Regions." College Math. J. 15, 433-435, 1984.
Grünbaum, B. "Venn Diagrams and Independent Families of Sets." Math. Mag. 48, 12-23, 1975.
Johnson, C. R. Book review. "Nonnegative Matrices in the Mathematical Sciences, by Abraham Berman and Robert J. Plemmons." Bull. Amer. Math. Soc. 6, 233-235, 1981.
Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., p. xii, 1995.
Perron, O. "Zur theorie der matrizen." Math. Ann. 64, 248-263, 1907.
Ruskey, F. "A Survey of Venn Diagrams." Electronic J. Combinatorics, Dynamical Survey DS5, June 18, 2005. http://www.combinatorics.org/Surveys/#DS5.
Ruskey, F. "Venn Diagrams." http://www.combinatorics.org/Surveys/ds5/VennEJC.html.
Ruskey, F.; Savage, C. D.; and Wagon, S. "The Search for Simple Symmetric Venn Diagrams." Notices Amer. Math. Soc. 53, 1304-1311, 2006. PDF
Shenitzer, A. and Steprans, J. "The Evolution of Integration." Amer. Math. Monthly 101, 66-72, 1994.
Venn, J. "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings." Dublin Philos. Mag. J. Sci. 9, 1-18, 1880.
Wikipedia. "Vesica_piscis."
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 43 and 873, 2002.