

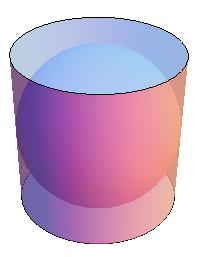
Cylinders
Charlie spies ANOTHER BLUEPRINT, another project (blueprint
of a cylindrical granary, ca. 5 meters high) --
CHARLIE
...What's this?
ALAN
We're converting the furnace to burn
renewable bio-mass fuel. Corn pellets.
PROFESSOR BILL WALDIE
Low-emission, reduces reliance on
foreign oil, 80 percent efficient.
CHARLIE
...You're putting a silo in our backyard?
ALAN
Cylindrical granary... To store the
corn. I was hoping you two would
help me with a geo-survey for the
site plan.
The term cylinder commonly refers to the solid of circular cross section in which the centers of the circles all lie on a single line (more properly called a circular cylinder). A cylinder is called a right cylinder if it is straight in the sense that its cross sections lie directly on top of each other; otherwise, the cylinder is said to be oblique.
|
|
To a mathematician, a cylinder extends to infinity in both directions along its axis. However, in common usage (including that of Charlie and Alan), it refers to a finite portion of the infinite surface. The cylinder was extensively studied by Archimedes in his two-volume work On the Sphere and Cylinder, in ca. 225 BC.
The lateral surface area and volume of the (finite) cylinder of height h and radius r (as illustrated above) are
The formula for the volume of a cylinder leads to the mathematical joke: "What is the volume of a pizza of thickness a and radius z?" Answer: pi z z a (i.e., π times z-squared times a). This result is sometimes known as the second pizza theorem.
Archimedes was aware of the remarkable fact that the ratio of a sphere's volume to the region lying between the circumscribed cylinder and sphere is exactly two, i.e.,
The geometry of this problem is also related to another attractive result relating the lateral surface area cut out of a sphere (known as a spherical segment) and cylinder by the same slicing planes--a result known as Archimedes' hat-box theorem.
The intersections of right circular cylinders give attractive and interesting shapes, the simplest examples of which (two left figures above) are known as the Steinmetz solid.
Bill Nye the Science Guy
Note that Professor Bill Waldie is played by Bill Nye the Science Guy. Bill Nye produced 100 episodes of his self-named show for PBS between 1993 and 1997 and was one of the original inspirations for NUMB3RS. He's already appeared in Episodes 211 ("Scorched"), 220 ("Guns and Roses"), and 308 ("Hardball"), and now 415 ("End Game").
OODA loops
CHARLIE
I got your message. About creating a
model for how two forces might engage
on a field of battle...
Charlie tosses a hefty ACADEMIC PAPER on the desk.
CHARLIE (cont'd)
...Someone's already done the work.
Colby reads off the paper --
COLBY
Observe. Orient. Decide. Act.
CHARLIE
It's an OODA (oo-duh) Loop.
Developed by a military strategist to
refine the art of aerial combat.
COLBY
...I'm strictly a ground guy.
CHARLIE
It'll work there, too. The idea is
simple. To defeat an enemy, one must
confine one's decision-making to a
cycle -- observe, orient, decide,
act.
The OODA loop is a concept and strategy originally proposed by U.S. Air Force Colonel John Boyd. It is the dominant model of military command and control, and is part of the military doctrine of all four branches of the U.S. Armed Forces, as well as of that of many other armed forces, including Sweden. As described by Charlie, the OODA loop consists of four overlapping processes: Observe, Orient, Decide, and Act.
While OODA finds widespread use as a military doctrine, it has nonetheless been described by researchers such as Berndt Brehmer as fundamentally inadequate as a model of command and control, particularly because it has very limited use as a basis for the design of new systems. Furthermore, while authors such as David Ullman have extended the OODA doctrine to more general sorts of decision making, OODA is not itself a mathematical or scientific concept. It is therefore not clear that it has much relevance to mathematical or scientific problem-solving or research, except perhaps as a very general framework within which such work may be carried out.
Caltrops and hyperbolic tetrahedra
Porter reaches for his OJ, knocks his burrito onto the
ground. He bends down, picks it up, looks at it. Disgusted.
CLAY PORTER (cont'd)
If I talk to you two anymore, I'll
lose the rest of my breakfast.
Porter tosses his food in the trash, goes to his motorcycle.
David and Colby toss their food, get in the car, start it up.
Porter pulls away. David and Colby follow, hear a POP! The
car pitches. They jump out, take a look... They see a flat
tire, HOMEMADE TIRE SPIKES on the ground.
Tire spikes are generally the shape of a sharpened tetrahedron. During World War II, a four-pronged device called a caltrop was used for puncturing the tires of enemy vehicles. Hundreds of these nasty spiked tetrahedra can be tossed along a road, and each one will land with a spike pointing straight up. In addition, the shape itself permits maximum penetration of a tire. As discussed by Martin Gardner, the idea is not a new one; here is a quotation from the sixteenth century: "The Irishmen had strawed all alongst the shore a great number of caltrops of iron, with sharp pricks standing up, to wound the Danes in the feet." Oliver Wendell Holmes mentioned caltrops in 1858.

The hyperbolic tetrahedron
illustrated above is one form of a "spiky" tetrahedron. Effectively, hyperbolization with parameter
α means applying the map ![]() to all points on the surface of a
polyhedron. Positive values of α
generate sharp cusps along the edges (while negative values of α generate round bulbs at the centers of the faces).
to all points on the surface of a
polyhedron. Positive values of α
generate sharp cusps along the edges (while negative values of α generate round bulbs at the centers of the faces).

The figures above show hyperbolic versions of all the Platonic solids.

A decorated hyperbolic dodecahedron has been used as the Mathematica logo since Mathematica 2 (second image from left, above). The previous logo (leftmost figure above) was the cumulated icosahedron informally known as "spikey" and slightly resembling the polyhedron Charlie is holding on the back jacket of his book, The Attraction Equation, from Episode 406, "In Security."
Some plants have adopted a tetrahedral shape, perhaps as a deterrence to being trampled on. For example, the scientific name of the star thistle is Centaurea calcitrapa.
Statistical decision theory
DON
...So that's what's happening here?
CHARLIE
Not to that extreme. But applying
Statistical Decision Theory, I did
identify an X-factor.
LIZ
You are gonna tell us, right?
CHARLIE
We've been assuming Ferraro's
objective is to kill Clay Porter,
when in fact, he's trying to keep him
alive. He wants to capture him.
Why, I can't tell you. But what I
can tell you is where...
He puts up a map of L.A. Nine DISCREET RED "HOT ZONES" pop.
CHARLIE (cont'd)
Substituting a capture scenario for a
kill scenario, my analysis generated
probable "fields of battle" where
Ferraro and Porter will likely meet.
DON
Alright, good. Let's get eyes in
these areas, start looking.
"Statistical decision theory" is a loosely defined term referring to a number of statistical tools that can be used to evaluate risks and aid in rational decision making. We're not sure what Charlie means when he refers to an "X-factor," but happily Hollywood magic seems to suffice in the absence of more rigorous mathematical techniques.
Wind Power
Alan spreads out a new blueprint. Charlie and Amita look - -
AMITA
...A windmill?
ALAN
Wind turbine is the precise term.
PROFESSOR BILL WALDIE
Generates 1000 watts at 11 meters per
second, an easy 5 kilowatts per day.
Goodbye grid.
CHARLIE
That sounds great.
It turns out that Los Angeles winds are poor for a wind turbine, according to the detailed maps available from the U.S. Department of Energy, an overview of which is reproduced above.
In an earlier scene, Charlie studies home heating needs. A government site he could use is the Home Energy Saver site, which provides expected savings for upgrading a home's energy efficiency.
References
Brehmer, B. "One Loop to Rule Them All." In 11th ICCRTS: Coalition Command and Control in the Networked Area. Sept. 26-28, 2006.
Gardner, M. Sixth Book of Mathematical Diversions. Chicago, IL: University of Chicago Press, pp. 185-187, 1984.
Nyelabs. "Bill Nye The Science Guy." http://www.nyelabs.com/
Schechtman, G. M. "Manipulating The Ooda Loop: The Overlooked Role of Information Resource Management in Information Warfare." Master's thesis, Air Force Institute of Technology, 1996. [PDF]
Ullman, D. G. Making Robust Decisions: Decision Management For Technical, Business, and Service Teams. Victoria, British Columbia: Trafford Publishing, 2006.
Wikipedia. Decision Theory, OODA Loop.