CHARLIE
          I think we're looking at "Angels
          and Devils."

                  FRALEY
          Excuse me?

                  CHARLIE
          M.C. Escher's print of angels and
          devils, an example of the figureground
          effect in perceptual organization.

Enter Audience Vision:

ESCHER'S CIRCLE LIMIT IV.  An interlocking B&W pattern of
BLACK DEVILS --

                  CHARLIE (V.O.) (cont'd)
          How we look at things is often
          determined by our predisposition.
          In the case of Escher's "Angels and
          Devils", one either can see figures
          of black devils --

Shifting perspective ever so slightly -- print becomes an
interlocking pattern of WHITE ANGELS.

                  CHARLIE (V.O.) (cont'd)
          -- or white angels.  Our perception
          is largely influenced by our
          thinking.

Figure-ground

The principle of figure-ground is fundamental for psychologists who study perception. Depending on whether the white or black color is seen as the figure (foreground) or the ground (background), the brain interprets the picture as two different images. Figure-ground illusions were discussed in Episode 406, "In Security."

Wallpaper groups

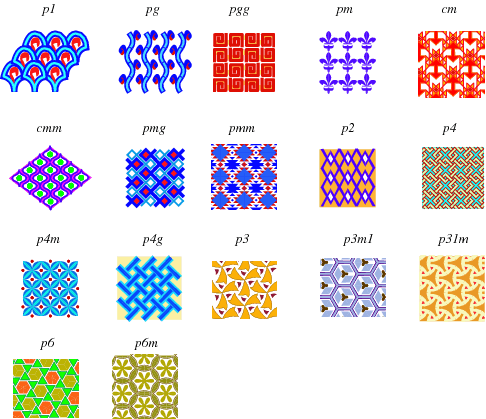
The Dutch artist M. C. Escher is well-known for artwork that incorporates high degrees of symmetry. His work "Angels and Devils" is just one of many in which artistic motifs are repeated in a regular pattern corresponding to various symmetry patterns in the plane. The mathematics of symmetry is known as group theory, and the particular types of symmetry that are possible in the plane are known as the wallpaper groups. There are exactly 17 such groups, illustrated above.

Beautiful patterns created with Artlandia SymmetryWorks based on several of the wallpaper groups are illustrated below.

Hyperbolic geometry

A hyperbolic geometry is a non-Euclidean geometry, also called Lobachevsky-Bolyai-Gauss geometry, and has a constant "sectional curvature" of -1. This geometry satisfies all of Euclid's postulates except the parallel postulate, which is modified to read: For any infinite straight line L and any point P not on L, there are many other infinitely extending straight lines that pass through P and do not intersect L.

In hyperbolic geometry, the sum of angles of a triangle is less than 180 degrees, and triangles with the same angles have the same areas. Furthermore, not all triangles have the same angle sum (cf. the AAA theorem, for triangles in the Euclidean plane). There are no similar triangles in hyperbolic geometry. The best-known example of a hyperbolic space are spheres in Lorentzian four-space. The Poincaré hyperbolic disk is a hyperbolic plane. Note that hyperbolic geometry is well understood in two dimensions, but not in three dimensions.

The Poincaré hyperbolic disk, illustrated above, is a model for hyperbolic geometry in which a line is represented as an arc of a circle whose ends are perpendicular to the disk's boundary (and diameters are also permitted). Two arcs that do not meet correspond to parallel rays, arcs that meet orthogonally correspond to perpendicular lines, and arcs that meet on the boundary are a pair of limits rays. The illustration above shows a hyperbolic tessellation similar to M. C. Escher's 1960 woodcut "Circle Limit IV (Heaven and Hell)," that can be regarded as the hyperbolic analog of "Angels and Devils." The animation at the top of this page illustrates the results of using the symmetries of hyperbolic geometry to produce beautiful kaleidoscopic patterns.

References

Artlandia. "Artlandia: Practical, Easy-to-Use Tools for Graphic Design." http://www.artlandia.com

"M. C. Escher: The Official Website." http://www.mcescher.com