Upchurch takes in the scene.

                   UPCHURCH (cont'd)
          ... but the big money snatches tend
          to put you in contact with a higher
          class of lowlife.  If they know
          their business -- and it looks to
          me like they do -- we'll be looking
          at simultaneous movement, expected
          payoffs, bargaining strategies...
          lots of variables.

                   CHARLIE (O.S.)
          What you're talking about is
          imperfect information games.

They turn to see CHARLIE, walking up --

Tabu search

                   CHARLIE
          You got it.  Assuming that the
          kidnappers are experienced -- or
          have benefited from the experience
          of other kidnappers -- we might use
          an optimization method called a
          Tabu Search.
             (off Upchurch's look)
          It's a way to exclude bad data --
          the places the kidnappers won't go
          -- to isolate where they will.

                   UPCHURCH
          I guess that's why they call it
          "tabu."

                   CHARLIE (cont'd)
          Charlie nods, then --

          The kidnappers are really... like a
          group of hikers --

AUDIENCE VISION -

A group of hikers check a map, a DESTINATION circled -- then
start marching through the woods --

The hikers trek along a trail -- past beautiful glades,
avoiding dangerous cliffs, heading toward the waterfall --

                   CHARLIE (V.O.) (cont'd)
          A Tabu Search will pinpoint the
          optimal route the hiker's will
          choose...

The essential idea of a tabu search (which is a category of so-called meta-heuristics) is to "forbid" search moves to points already visited in the search space, at least for the upcoming few steps. In a tabu search, one therefore allows new inferior solutions to be temporarily accepted in order to avoid paths already investigated. This approach can lead to exploring new regions of the space of all possible solutions, with the goal of finding a solution by globalized search. Tabu search has traditionally been applied to combinatorial optimization (e.g., scheduling, routing, traveling salesman) problems. The technique can be made, at least in principle, directly applicable to continuous global optimization problems by a discrete approximation of the problem, but other extensions are also possible.

In light of the above, the scenario described in Charlie's analogy is not really a tabu search. A better example of a tabu search might be a technique sometimes used by computers to solve mazes constructed on a square grid with straight walls. (For some commentary on mazes, see the Math Notes from Episode 406, "In Security.") In this approach, the height of a square is increased by one each time it is visited, and subsequent explorations are made by following the path with the lowest height at each step. This approach can be visualized as building up a set of ramps, then always traveling in the downhill direction until either the exit of the maze or a local minimum is reached.

Furthermore, since there are so many variables to take into account, the tabu search Charlie wants to use must also operate in a very high-dimensional space (where each variable can be considered a single dimension). There are many different things that Charlie could predict: how, when, how much money the kidnappers want, what other things they might want, how they will behave in case they don't get what they want, and so on. In general, searches in very high-dimensional spaces are notoriously difficult (this phenomenon is known as the "curse of dimensionality"). Charlie might therefore be wise to use a few other mathematical techniques in addition to, or in preparation for, doing a tabu search.

In particular, Charlie could reduce the problem to a simpler lower-dimensional one by carrying out a Karhunen-Loeve decomposition (principle component analysis), or by using functional analysis techniques to embed the problem in an infinite-dimensional problem. Interestingly, many problems become easier to solve in infinitely many dimensions than in many dimensions. The whole theory of Hilbert spaces and Banach spaces deals with this infinite-dimensional case. We'll comment more on infinite-dimensional spaces in a forthcoming episode.

Bayesian priors

                   CHARLIE
          The ransom negotiation cut short,
          so I'm going to need to re-think my
          Tabu Search.
              (checks his papers)
          Maybe if I weight the data with a
          Bayesian prior --

Bayesian priors are an advanced topic in probability theory. To understand Bayesian priors, first consider the question, "Will the weather be cloudy tomorrow?" A prediction can be made based on past history by estimating P(cloudy), the probability that the skies will be cloudy, by the fraction of cloudy days that followed all similar previous days, N(cloudy)/N(total similar). While a so-called frequentist approach might stop there, a Bayesian approach would try to make a theory about the weather. Let P(theory|data) be the conditional probability of the theory given the data. From there, Bayes' theorem can be used:

Here, P(theory) is the prior confidence that the theory was true. Both the theory and the confidence can be adapted. For a spam filter, the theory is used to assign confidences to a message, usually based on the vocabulary, programming, and source of the message. As an example, large flashing red text is a strong spam indication. Training a Bayesian spam filter has two aspects. First, flagging a message as spam will strengthen the Bayesian prior, P(theory). Second, flagging a false positive will modify and strengthen the theory.

Heron's fountain

Charlie, carrying files and papers under his arm, enters to
find Amita helping LARRY tweak the height of the main chamber
on Larry's HERO'S FOUNTAIN (an apparatus made of two
vertically stacked jars, half filled with water, and
connected by an air hose and a funnel).  All centered in a
Zen Rock Garden.

                   CHARLIE
          Please tell me you didn't buy that
          in a head shop.

Larry looks askance --

                   LARRY
          Actually, Charles, you can't find
          this in any shop.  I've constructed
          my own Hero's Fountain.

OFF Charlie's look --

                   AMITA
          ...Named for Hero of Alexandria.
          The Greek mathematician and
          engineer.  Once we get the pressure
          right, the water will start to flow
          under its own power.

                   CHARLIE
          And how's this part of your
          achieving Zen?

Hero (or Heron) of Alexandria was a mathematician and engineer who lived AD 10-70. Among other items, he invented the first steam engine, the first vending machine, and the first windmill. Hero's fountain is now a classic demonstration of both hydraulics and pneumatics.

Heron's formula

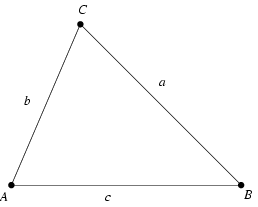
In mathematics, Heron is perhaps best known for Heron's formula, which gives the area of a triangle in terms of the lengths of its three sides. This formula is also known as Hero's formula. Given the lengths of the sides a, b, and c and the semiperimeter (i.e., half the perimeter),

of a triangle, Heron's formula gives the area Δ as

Heron's formula may be stated beautifully using the general formalism of the Cayley-Menger determinant:

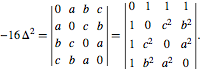
Here, the object delimited by vertical bars is an important mathematical construct in linear algebra known as a determinant. The value of a 2×2 determinant is defined to be

A k×k determinant can be expanded "by minors" to obtain

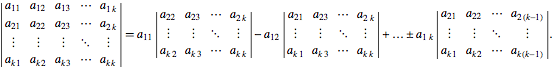
A so-called minor of A is obtained by taking the determinant of A with row i and column j crossed out.

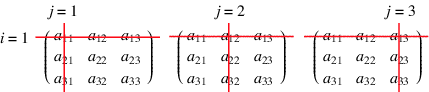
For example, for a 3×3 matrix, the above formula gives

The procedure can then be iteratively applied to calculate the minors in terms of subminors, etc.

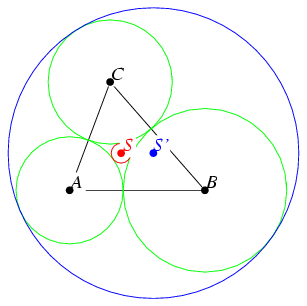
Expressing the side lengths a, b, and c in terms of the radii a', b', and c' of the mutually tangent circles centered on the vertices (which define the Soddy circles)

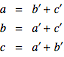
gives the particularly pretty form

Heron's proof is ingenious but extremely convoluted, bringing together a sequence of apparently unrelated geometric identities and relying on the properties of cyclic quadrilaterals and right triangles. Heron's proof can be found in Proposition 1.8 of his work Metrica (ca. 100 BC-AD 100). This manuscript was lost for centuries until a fragment was discovered in 1894 and a complete copy in 1896. More recently, writings of the Arab scholar Abu'l Raihan Muhammed al-Biruni have credited the formula to Heron's predecessor Archimedes (whose accomplishments we discussed in the Math Notes for Episode 403, "Hollywood Homicide"), prior to 212 BC.

A much more accessible algebraic proof proceeds from the law of cosines:

Then

giving

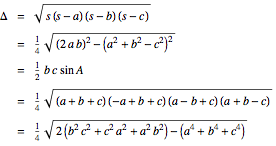
Heron's formula contains the well-known Pythagorean theorem as a degenerate case.

Minimax theorem

                   CHARLIE
          I think what he's trying to say is
          Pierce has violated his own rules of
          corporate Game Theory.  It's standard
          Minimax -- like a tug of war --

BEGIN AUDIENCE VISION -- TWO TEAMS OF EIGHT align at opposite
ends of a rope --

                   CHARLIE (V.O.) (cont'd)
          -- a demonstration of brute strength
          by two opposing groups.  The object
          being to pull one's opponent across
          the center line first.

In a spirited display, both teams pull on the rope -- taut.

                   CHARLIE (V.O.) (cont'd)
          However, after the competition
          begins --

Both teams are evenly matched, the rope barely budging in
either direction.

          -- one team can embarrass the other
          by letting go of the rope--

One team releases the rope -- the other team jerks their end
and falls flat on their asses.  The other team laughs.

                   CHARLIE (V.O.) (cont'd)
          That team humiliates their
          opposition... but they've lost.

The team pick themselves up and celebrates their win -- END
AUDIENCE VISION.

                   CHARLIE (cont'd)
          Pierce has let go of the rope...
          struck back in the way least likely
          to achieve a positive result.

The minimax theorem (where minimax refers to minimization of the maximum result obtained by another player) is the fundamental theorem of game theory. It states that every finite, zero-sum, two-person game has optimal mixed strategies. (Here, a mixed strategy is a collection of moves together with a corresponding set of weights that are followed probabilistically in the playing of a game.) The minimax theorem was first proved by the famous mathematician and father of modern computing, John von Neumann, in 1928.

To state the theorem formally, let X and Y be mixed strategies for players A and B and let A be the payoff matrix. Then

where v is called the value of the game and X and Y are called the solutions. It also turns out that if there is more than one optimal mixed strategy, there are infinitely many.

In the closing scene of the Season 4 opening episode "Trust Metric," Charlie mentioned that he used the minimax theorem in an attempt to derive an equation describing friendship.

Minimax approximations

In general, a minimax approximation is a minimization of the maximum error for a fixed number of terms. In approximation theory, the most common minimax approximation is the minimax polynomial, which gives the approximating polynomial that has the smallest maximum deviation from the true function. Such polynomials are closely approximated by the Chebyshev polynomials of the first kind T_n(x). Minimax polynomials are illustrated in the animation at the top of this page for a particular function in the complex plane.

Cake-cutting theory

                   UPCHURCH
              (re: decoder)
          Not quite what I imagined reading
          your more ethereal musings on Cake-
          Cutting Theory, Professor.

                   CHARLIE
          Sometimes cake is a series of
          algorithms to formulate an
          analysis.  And sometimes cake is
          just... cake.

The study of fair division problems is known as cake-cutting theory. It can be mathematically shown that it is always possible to "fairly" divide a cake among n people using only vertical cuts. Furthermore, it is possible to cut and divide a cake such that each person believes that everyone has received 1/n of the cake according to his (or her) own measure. Finally, if there is some piece on which two people disagree, then there is a way of partitioning and dividing a cake such that each participant believes that he has obtained more than 1/n of the cake according to his own measure.

The general cake-cutting method for two people (say, Alice and Bob) is that Alice cuts the cake, and Bob chooses which piece he wants ("divide and choose").

For three people (Alice, Bob, and Carl), Alice cuts one piece, Bob cuts the remainder, and Carl then chooses one of the three pieces. Alice then makes adjustments on the remainder, and Bob chooses. Alice gets the last plate.

Ignoring the height of the cake, the cake-cutting problem is really a question of fairly dividing a circle into n equal-area pieces using cuts in its plane. One method that proves fair cake cutting is always possible relies on the Frobenius-König theorem, which is a beautiful result in combinatorial matrix theory that is probably one of Amita's favorites!

Determining the maximum number of pieces in which it is possible to divide a circle for a given number of cuts is called the circle cutting or pancake cutting problem. (For another mathematical pancake problem, and one with a very surprising contributor to the research literature on the subject, see the pancake sorting problem.) The minimum number of pieces is always n + 1, where n is the number of cuts, and it is always possible to obtain any number of pieces between the minimum and maximum. The first cut creates 2 regions, and the nth cut creates n new regions, so it can easily be shown that the maximum number of pieces is given by (n² + n + 2)/2.

The problem of dividing a circle by lines can also be generalized to dividing a plane by circles. As can be seen above, the maximal numbers of regions obtained from n = 1, 2, 3, 4, ... circles are given by 2, 4, 8, 14, .... The astute reader may note that the n = 3 case looks strangely familiar. In fact, this configuration corresponds to the most commonly encountered case of a Venn diagram, a subject on which we will have more to say in the Math Notes for Episode 412, "Power." The alert reader may also be interested in attempting to derive the simple formula giving the maximal number of regions obtained for n circles (if so, you may wish to refrain from clicking the links above until you have obtained your solution).

Of course, dividing the plane by circles can also be generalized to dividing a plane by ellipses, where ellipses have been previously discussed in the math notes for Episode 401, "Trust Metric." The maximal numbers of regions obtained from n = 1, 2, 3, 4, ... ellipses are given by 2, 6, 14, 26, .... There is again a very simple formula giving the maximal number of regions.

While Charlie can probably solve intersection-maximizing problems in his head, they can require great ingenuity for people with lesser gifts. In particular, consider the more challenging problem of cutting a cylinder into a maximum number of pieces by n oblique cuts.

References

Barlow, R. Developments in Bayesian Priors. 2005.

Brams, S. J.; Jones, M. A.; and Klamler, C. "Better Ways to Cut a Cake." Not. Amer. Math. Soc. 53, 1314-1321, 2006.

Brams, S. J. and Taylor, A. D. "An Envy-Free Cake Division Protocol." Amer. Math. Monthly 102, 9-19, 1995.

Brams, S. J. and Taylor, A. D. Fair Division: From Cake-Cutting to Dispute Resolution. New York: Cambridge University Press, 1996.

Glover, F. and Laguna, M. Tabu Search. Dordrecht, Netherlands: Kluwer, 1996.

Glover, F.; Taillard, E.; and De Werra, D. "A User's Guide to Tabu Search." Ann. Oper. Res. 41, 3-28, 1993.

Osman, I. H. and Kelly, J. P. (Eds.). Meta-Heuristics: Theory and Applications. Dordrecht, Netherlands: Kluwer, 1996.

Piwakowski, K. "Applying Tabu Search to Determine New Ramsey Numbers." Electronic J. Combinatorics 3, No. 1, R6, 1-4, 1996. http://www.combinatorics.org/Volume_3/Abstracts/v3i1r6.html

Robertson, J. and Webb, W. Cake Cutting Algorithms: Be Fair If You Can. Wellesley, MA: A K Peters, 1998.

Stromquist, W. "How to Cut a Cake Fairly." Amer. Math. Monthly 87, 640-644, 1980.

Venn, J. "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings." Dublin Philos. Mag. J. Sci. 9, 1-18, 1880.

Voss, S.; Martello, S.; Osman, I. H.; and Roucairol, C. (Eds.). Meta-Heuristics: Advances and Trends in Local Search Paradigms for Optimization. Dordrecht, Netherlands: Kluwer, 1999.